Интеллектуальное развитие обучающихся средствами сетевого проекта по математике

Современное определение цели  школьного образования, его результатов (предметных, метапредметных, личностных) выводит на передний план задачу интеллектуального развития человека,  включающего, в частности, его способности к усвоению новых знаний, к самостоятельному поиску и усвоению новой информации [1]. Современное общество нуждается в личности, обладающей самостоятельностью и оригинальностью суждения, остроумием и глубокомыслием,  способной к продуктивному мышлению. Эффективное решение этой задачи объективно невозможно без создания определенных условий, благоприятствующих  становлению и развитию интеллектуальных способностей каждого ученика, укреплению индивидуального  своеобразия его ума [3].  

В последнее время особая роль в интеллектуальном развитии  отводится телекоммуникационному (сетевому) проекту.  Проектная деятельность стимулирует  самообразование, способствует формированию умения работать с научными текстами, использовать индивидуальные способы кодирования информации, тем самым создавая условия для развития различных форм умственного опыта  участников проекта – понятийного, когнитивного, метакогнитивного и эмоционально-оценочного.  Привлечение  телекоммуникационных ресурсов создает дополнительные  условия  для развития интеллектуальных возможностей  школьников, формирования у них индивидуального ментального  (умственного)  опыта. Как единое целое сетевой проект  по своему содержанию  и технологическому воплощению становится для каждого участника своеобразной «интеллектуальной нишей», дающей ему шанс  на личную  интеллектуальную жизнь, - независимо от места проживания и учебного учреждения [3].

С целью создания условий для индивидуального интеллектуального развития обучающихся  через освоение определенным образом организованного предметного содержания, через продвижение  в этом содержании и последующее порождение новых форм этого предметного содержания разработан сетевой  математический проект  «Пьер Ферма: универсальный гений». 

Начиная работу над проектом, авторский коллектив уже имел за плечами опыт разработки и реализации двух региональных сетевых проектов по математике: "Через века и страны: в поисках функции" [4] и "Числительные и меры: математическое многоборье" [5].

История математики содержит немало удивительных страниц. Приоткроем одну из них и  окажемся в 17 веке. Именно тогда Пьер Ферма сформулировал загадочное утверждение, доказательство которого математики всего мира искали 350 лет. Это утверждение стало известно как Великая теорема Ферма. Попытки ее доказательства обогатили математику новыми идеями, методами, теориями.

Данный проект и был посвящен этому одному из крупнейших математиков в истории науки  - французу Пьеру Ферма, которого уже в 17 веке многие считали гением. Проект  объединил  всех любителей математики и ее истории. Участники  проекта окунулись в мир поиска и исследования, освоили интересные сервисы. 
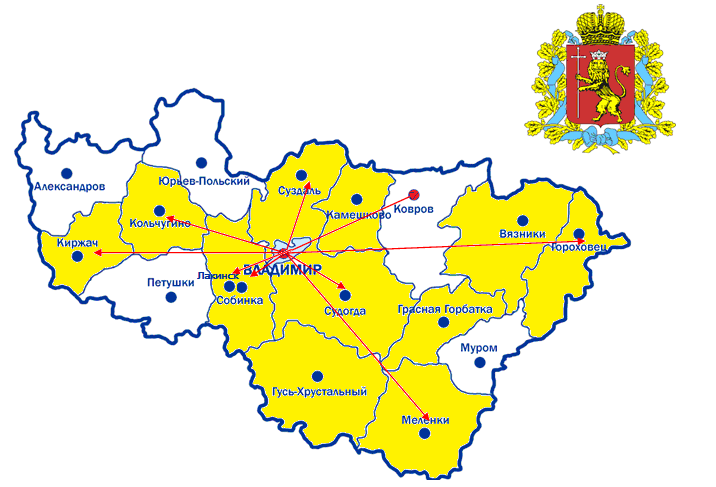
Проект охватил 13 из 21 (62 %) муниципальных образований Владимирской области, в том числе 9 городов и 11 поселков, деревень и сел (г. Владимир, Вязниковский, Гороховецкий, Гусь-Хрустральный, Камешковский, Киржачский районы, г. Ковров, Кольчугинский, Меленковский, Селивановский, Собинский, Судогодский, Суздальский районы). Участниками проекта стали также команды из Тамбовской области и г. Таллина  (Эстония).

 

В проекте принял участие 101 обучающийся (в 23 командах был 81 участник, а  20 ребят стали индивидуальными участниками). Руководителями команд и индивидуальных участников были 48 учителей (35 учителей математики, 6 учителей информатики, 4 учителя математики и информатики, 2 учителя математики и физики, 1 учитель математики, физики и информатики).

Участникам проекта необходимо было ответить на основополагающий вопрос: « Как стать великим?»; найти ответы на проблемные вопросы: «Какое влияние на развитие математики оказал Пьер Ферма?», «Кто из математиков мира внес больший вклад в доказательство теоремы Ферма?», «Каковы методы решения неопределенных уравнений первой и второй степеней?», а также изучить учебные вопросы: «Какие уравнения  называются диофантовыми?», «Какие уравнения называются неопределенными?», «Что означает выражение «попарно взаимно просты»?», «Каково свойство деления с остатком?», «В чем суть алгоритма Евклида?», «Какие дроби называют цепными?», «В чем заключается метод рассеивания или размельчения?».

Участие в математическом проекте - это не только и не столько соревнование любителей математики, но в первую очередь - приобщение к научному исследованию, знакомство с лабораторией научного труда. Чтобы добиться высокого результата, надо каждому участнику проекта развивать в себе  определенные умения  и качества: личную  ответственность и гибкость в различных ситуациях;  установление высоких стандартов и целей для себя и для других; терпимость к другим точкам зрения; коммуникативные умения; творчество и любознательность, открытость  новым точкам зрения; критическое и системное мышление; понимание взаимосвязей в сложных системах; умение работать с информацией и медиа-средствами; умение устанавливать межличностное взаимодействие и сотрудничество, уважать различные мнения; направленность на саморазвитие; обладание  социальной ответственностью. Для развития в обучающихся перечисленных качеств авторами проекта была предложена система творческих заданий.

Каждое научное открытие связано с именем конкретного человека, о котором мы порой имеем самое малое представление.  Кто эти люди, создающие научные знания? Что ими движет, что заставляет вновь и вновь искать истину? На первом этапе    участникам проекта было предложено   рассмотреть не конкретного человека, а феномен человека науки, ученого: как он "двигает науку вперед", в чем заключается его специфическая деятельность,  порождающая новые знания, ради чего он это делает?

Как известно, Пьер Ферма имел удивительную судьбу. Он не стал "профессиональным" математиком, избрав для себя профессию юриста.  В свой бурный век он вел жизнь основательную и тихую, будучи домоседом и добросовестным государственным  чиновником. Ферма не писал философских трактатов, как Декарт, не был вхож к французскому королю, как Виет, не воевал, не путешествовал, не собирал вокруг себя и  сам не посещал математических кружков, не имел учеников и почти не печатался при жизни. Математика всегда оставалась для Ферма увлечением, хобби. И все-таки сегодня Пьера Ферма называют   одним из   титанов математики нового времени, заложившим основы многих ее областей.  На втором этапе проекта его участникам предстояло сформулировать гипотезу о влиянии работ Пьера Ферма на развитие математики и обосновать выдвинутую гипотезу, изучив биографию Пьера Ферма и составив ленту времени, выделив наиболее значительные события в жизни этого ученого. На основании проведенного исследования участники могли создать интерактивный кроссворд, посвященный Пьеру Ферма.  

Великая теорема Ферма сыграла выдающуюся роль в развитии математики. История поисков ее доказательства чрезвычайно романтична, много людей размышляли над ней, не один великий математик пытался ее доказать и потерпел неудачу.  Попытки доказательства, предпринимаемые с XVIII века, привели к созданию целого арсенала математических методов и средств. На третьем этапе проекта его участники  изучали историю доказательства Великой теоремы Ферма и составляли  ментальную карту, отражающую ее самые яркие страницы, рассуждали на страницах математического эссе о роли теоремы в истории математики, высказывали свое мнение о том, кто из математиков мира внес больший вклад в ее доказательство, давали обоснованный ответ на вопрос: «Принимали ли русские математики участие в попытках доказательства этой теоремы?» .

Любимой областью математики для Ферма была теория чисел, в которой он не имел себе равных.  Наставником и учителем, во многом вдохновившим Ферма на его исследования, стала "Арифметика" Диофанта. Древнегреческий мыслитель в своей книге рассматривал более сотни задач, многие из которых сводились к решению уравнений, в современной математике называемых диофантовыми (или неопределенными). Предложенные Диофантом методы решения неопределенных уравнений получили новую жизнь в работах знаменитых математиков, и прежде всего  Ферма. Теория диофантовых уравнений является одним из самых интересных и трудных разделов математики.  Самое крупное достижение математики последних лет – доказательство Великой теоремы Ферма, полученное англичанином Э. Уайлсом,  – относится именно к теории диофантовых уравнений. На четвертом этапе проекта его участники  составляли  электронное пособие для подготовки к олимпиаде по математике для  учащихся средней школы, в котором излагали виды и методы решения неопределенных уравнений первой и второй степеней, приводили примеры исторических задач, сводимых к решению диофантовых уравнений,  и алгоритмов  решения в целых числах разными способами одного из таких  уравнений.

Для выполнения каждого задания участникам был предложен для использования конкретный сервис web 2.0, освоение которого  не только развивало умение работать с информацией, но и способствовало формированию критического и системного  мышления, побуждало к творчеству.

В ходе реализации проекта его участниками были созданы разнообразные проектные продукты.

Одно из качеств интеллектуально развитой личности – умение  объективно оценить собственную деятельность. Поэтому наряду с внешней оценкой, необходимой  в каждом проекте, не менее важно было создать условия для оценки внутренней, формирующей: на  стадии вступления в проект - определяя свои интеллектуальные потребности; в ходе выполнения заданий -  развивая самостоятельность и взаимодействие; наблюдая за процессом исследования; проверяя понимание того, что делается; по завершению (ии) проекта - подтверждая понимание и  сформированные умения. Для организации данной работы авторами была организована Лаборатория проекта, участие в работе которой было обязательным условием для всех участников. Основные инструменты формирующего оценивания, используемые в Лаборатории:

Для всех, кому была нужна помощь, кто был готов поделиться с другими своими успехами в освоении новых сервисов, нуждался в общении,  в проекте был создан блог «Форум участников сетевого математического проекта». Приведем отзывы о проекте некоторых участников: «Вот и подошел к концу замечательный проект под названием «Пьер Ферма - универсальный гений»! Мы, команда ШК2ЛАМУС, хотим сказать спасибо организаторам этого конкурса, который стал для нас увлекательным путешествием в мир математики и позволил проявить творческую активность в рамках любимого школьного предмета. Работа над заданиями проекта была очень упорной, и каждый участник нашей команды принимал участие в их выполнении. Мы четко распределили обязанности каждого участника: подбирали интересный исторический материал все вместе (мы даже ходили в читальный зал библиотеки за достоверной информацией о жизни Пьера Ферма и о доказательстве его Великой теоремы), а вот различные эссе писали дружным тандемом девушек (своеобразный «мозг» нашей команды). … Проект сплотил нас! Будем с нетерпением ждать новых идей! Такой проект должен развиваться, а мы, новое поколение, вам в этом поможем! … Мы, команда ШК2ЛАМУС, не прощаемся с вами, а говорим «до свидания»!

Подводя итоги проекта, можно с уверенностью сказать, что  наш проект действительно создает все условия для решения новых задач современной школы.