Сущность творчества – в предугадывании результата правильно поставленного опыта, в создании усилием мысли рабочей гипотезы, близкой к действительности.
Люди совершают каждый день массу дел: маленьких и больших, простых и сложных. И каждое дело – задача, то более, то менее трудная. Но при всём их внешнем разнообразии, а иногда и несравнимости все дела можно разделить на две группы – старая это задача или новая.
Диапазон творческих задач необычайно широк по сложности – от решения головоломки до изобретения новой машины или научного открытия, но суть их одна: при решении происходит акт творчества. Вот здесь-то и требуются особые качества ума, такие, как наблюдательность, умение сопоставлять и анализировать, комбинировать, находить связи и зависимости, закономерности и т. д. – всё то, что в совокупности и составляет творческие способности.
Сегодня школа призвана готовить подрастающее поколение к жизни и труду в современных условиях, для которых характерны состязательность и конкуренция, возрастающие требования к качеству труда. В этих условиях учебно-воспитательный процесс в школе должен быть направлен на выполнение нового социального заказа – на формирование творческой социально-адаптированной личности, её способности к творчеству в самых разнообразных сферах деятельности.
Чем актуальнее потребность общества в творческой инициативе личности, тем острее необходимость в теоретической разработке проблем творчества, изучении его природы и форм проявления, его источников, стимулов и условий.
Креативность – способность порождать необычные идеи, отклонение от традиционных схем мышления, быстро решать проблемные ситуации [1].
П. Торрес под креативностью понимает «… копать глубже, смотреть лучше, исправлять ошибки, нырять в глубину, беседовать с кошкой, проходить сквозь стену, зажигать солнце, строить замок на песке, приветствовать будущее».
Д. Гильфорт определил 4 особенности креативного мышления:
- оригинальность и необычность высказываний, стремление к новизне;
- семантическая гибкость мышления (способность видеть объект под разными углами зрения);
- образная адаптивная гибкости (способность изменить восприятие объекта таким образом, чтобы видеть его новые или скрытые стороны);
- способность продуцировать разнообразные идеи, чтобы активировать творческое мышление младших школьников (он рекомендует использовать «Мозговой штурм») [2].
Развитие учащегося, как личность, как субъект деятельности является значимой проблемой образования на данный момент. Это связано с тем, что в наше время возросла потребность в тех людях, которые смогут быстро адаптироваться в учебном, а затем и в трудовом коллективе, проявляя самостоятельность и инициативу в работе.
Развитие креативного мышления, во-первых, способствует осознанному получению знаний и стремлению к их самостоятельному «добыванию», умению применять их в своей практической деятельности.
Во-вторых, креативное мышление необходимо как для разрешения противоречий и проблемных ситуаций в учебном процессе, так и для успешного решения жизненных, не учебных задач.
В-третьих, благодаря креативному мышлению и умению нестандартно, по-новому мыслить, современный специалист является конкурентно-способной личностью, поэтому креативное мышление нужно развивать у каждого школьника-будущего специалиста.
К сожалению, в современной школе, особенно по традиционной программе, развитию креативного мышления детей уделяется пока ещё крайне мало времени. Одной из форм его развития являются творческие задачи. C недавнего времени я начала работать по этой программе и использую их в своей работе.
Опыт показывает, что уроки математики очень оживляют учебные задания творческого характера, связанные с их составлением и преобразованием, способствующие реализации не только образовательных, но и развивающих целей. Использование творческих заданий отличается тем, что принимает форму игровой деятельности, что очень привлекательно именно для младшего школьника. Успех при выполнении задания пробуждает интерес к учёбе, создаётся эмоциональный положительный фон.
В психолого-педагогической науке неоднократно отмечалось то, что сейчас, в условиях стремительно нарастающей информации, особое значение приобретает развитие и активизация творческого мышления. Действительно, в любой деятельности становится особо важным не просто усвоить определённую сумму знаний, а выбрать наиболее значимые из них, суметь применить их при решении самых различных вопросов.
Исследования творческого мышления стали расширяться во второй половине XX века. Были составлены первые диагностические задания, выявляющие уровень развития творческого мышления. Стали экспериментально изучаться процессы творчества детей и подростков. Разрабатывались первые учебные программы формирования творческих способностей. В это время были выявлены психологические составляющие творческой деятельности: гибкость ума; систематичность и последовательность мышления; диалектичность; готовность к риску и ответственности за принятое решение.
Гибкость умавключает способность к выделению существенных признаков из множества случайных и способность быстро перестраиваться с одной идеи на другую. Люди с гибким умом обычно предлагают сразу много вариантов решений, комбинируя и варьируя отдельные элементы проблемной ситуации.
Систематичность и последовательность позволяет людям управлять процессом творчества. Без них гибкость может превратиться в «скачку идей», когда решения до конца не продумываются. В этом случае человек, имеющий много идей, не может выбрать среди них. Он не решителен и зависим от окружающих людей. Благодаря систематичности все идеи сводятся в определенную систему и последовательно анализируются. Очень часто при таком анализе, на первый взгляд, абсурдная идея преобразовывается, и открывает путь к решению проблемы.
Творчески мыслящий человек также нуждается в способности рисковать и не бояться ответственности за своё решение. Это происходит потому, что часто старые и привычные способы мышления более понятные большинству людей [3].
Можно ли добиться того, чтобы ребёнок стал «умнее», «способнее», «одарённее»? Конечно, если развитием умственных способностей заниматься так же регулярно, как тренируются в развитии выносливости, силы и других подобных качеств. Если ребёнок постоянно тренирует свой ум, решает трудные задачи, действует активно, самостоятельно находит верные решения в нестандартных ситуациях – результат обязательно будет [4].
Как известно, неспособных детей нет, нужно просто помочь ребёнку развить его способности, сделать процесс увлекательным и интересным. Главное начать как можно раньше и результат можно будет увидеть уже в конце 1 класса. Постоянно возникает вопрос «Нужна ли олимпиада по математике в начальной школе?» Необходима. Но как в условиях традиционной программы подготовить детей? Нельзя ограничивать детей школьной программой. Надо раскрепостить мышление ученика, использовать те богатейшие возможности, которые дала ему природа. Поэтому я считаю, что можно даже на уроке найти 5–10 минут на решение нестандартных задач, развивающих логику и смекалку, направленных на развитие творчества ребёнка. Такие занятия помогают сформулировать собственную точку зрения, воспитывают в детях доверие к собственным силам и интерес к другому мнению, учат культуре общения. Очень хорошо если этому можно посвятить целый урок. Способствует развитию креативности и факультативные занятия. Немало важной ступенью в развитии креативного мышления является обучение решению задач познавательного, поискового и творческого характера.
Виды творческих задач
Обычно в школе решают так называемые «закрытые» задачи, т. е. имеющие точное условие, строгий алгоритм решения, единственно верный ответ. Жизнь же ставит перед человеком «открытые» задачи, имеющие довольно размытые, разные пути решения. Исходя из этого, существуют следующие виды творческих задач.
Изобретательская.
Её условие содержит противоречие: «Вы хотите есть. На столе хлеб, а у стола голодный лев». Как быть? Ответы детей:
- вызвать служащих зоопарка;
- зажечь факел и испугать льва огнём;
- бросить льву кость или мясо;
- может это не животное, а человек.
Решение этой задачи показало, что дети видят разные варианты решений.
Исследовательская.
Произошло некоторое явление. Необходимо выявить его причины. Например, почему вода превращается в лёд? Как это происходит? Почему?
Конструкторская.
Не содержит противоречий и предлагает продумывание устройств под заданную цель. Придумать, как измерить площадь фигуры, тогда как дети ещё не имеют представления о самом понятии «площадь».
Прогностическая.
Предлагает анализ положительных и отрицательных последствий известных всем явлений или можно видоизменить обычную задачу и прогнозировать результат.
Задача с достраиваемым условием.
Дети анализируют и сами вводят необходимые данные и ограничения. К первоначальному этапу отношу задания на сравнение геометрических фигур, на выбор сходных фигур, на выделение частей сложного чертежа, на составление и преобразование фигур в соответствии с условием задачи, на составление рассказов к рисункам. Конечно, задачи 1 и 2 вида (исследовательские и изобретательские) едва ли будут уместны на каждом уроке математики. Их я использую на уроках окружающего мира, чтения, труда, а на уроках математики – в разминках и минутах отдыха, организованных в форме «мозгового штурма».
«Мозговой штурм» является методом, позволяющим снять психологическую инерцию и получить максимальное количество новых идей в минимальное время. При проведении «мозгового штурма» запрещается критика и поощряется любая идея, даже шуточная и явно нелепая. С целью активизации мышления младших школьников можно использовать следующие задания [5].
Задача № 1
Сгорело деревянное строение на берегу моря в лесу. Откуда пришёл огонь? Ответы детей: подожгли дети; курящий мужчина бросил сигарету; туристы не потушили костёр; в избушку ударила молния и т. д.
Задача № 2
У К. Чуковского в книге «Доктор Айболит» встречается Тянитолкай – фантастическое животное с двумя головами, расположенными сзади и спереди. Скажите, какие преимущества появились у Тянитолкая благодаря этому качеству? Ответы детей: способность постоянно бодрствовать, так как головы спят по очереди; быстрее ест; видит всё, что находится вокруг; имея две головы, веселее жить; животное лучше видит и слышит, а значит, может вовремя заметить опасность.
Задача № 3
Игра «Остров»
Представьте себе, что произошло кораблекрушение и вы, чудом уцелев, оказались на необитаемом острове в южных широтах океана. Что необходимо делать, чтобы выжить?
Ответы детей: необходимо строить жильё, охотиться, ловить рыбу, охранять лагерь.
Второй метод активизации мышления, называется «Синектика». Автор этого метода Уильям Дж. Гордон выделил два вида процессов творчества: интуиция, вдохновение и использование различных видов аналогии.
Широко распространена аналогия по форме, например:
Сосулька – карандаш, нож, перчатки, ручка, нос, клюв. Часы – луна, солнце, цветок, диск телефона, тарелка.
Для знакомства детей с прямой аналогией можно использовать художественные произведения. Например:
Фантастические аналогии позволяют отказаться от стереотипов, снять психологическую инерцию, пойти неизвестным ранее путём. Она способна любую ситуацию, любое действие перевести в сказку и рассматривать волшебство, фантастических и сказочных зверей, насекомых. Пришельцев с других планет для решения задач, для выхода из создавшейся ситуации.
К прямой аналогии относится и функциональная аналогия: надо определить, какие функции выполняет объект, а потом в окружающем мире найти объект, который выполняет такие же функции. Например:
Ветер – вентилятор, пылесос, дыхание. Петух – будильник, радио, солнышко, гром.
Машина – лошадь, ослик, муравей, поезд, сороконожка, велосипед, птица.
Примеры заданий на развитие креативности мышлений
Задания на развитие гибкости мышления.
- Разработать несколько способов использования законов и явлений.
- Установить взаимосвязи между изучаемым материалом и конкретным заданием:
- вычленить проблему;
- составить план решения;
- сформулировать гипотезы;
- выбрать и обосновать лучший способ решения.
Задания на развития оригинальности мышления.
- Определить «правильность» решения задачи.
- Придумать слово, необычную задачу.
- Предложить совершенно иной способ решения задачи.
Выполняя подобные задания, мои ученики с удовольствием находят недочёты в предлагаемых мной заданиях, придумывают свои варианты, в том числе задачи с фантастическими, несуществующими персонажами. Для лучшего усвоения новой темы составляем вместе сказку о том, как родилась линия.
«В стране Геометрия жила-была точка (учитель показывает на доске, а дети на листочках бумаги ставят точку). Однажды точка подумала: «Как мне хочется иметь много друзей! Отправлюсь-ка я в путешествие и поищу себе подружек».
Только вышла красная точка за калитку, а навстречу ей идёт зелёная точка. Подходит зелёная точка к красной и спрашивает, куда та идёт.
Иду искать друзей. Вставай рядом со мной и идём вместе путешествовать. (Учитель и дети ставят рядом с первой вторую точку).
Через некоторое время они встречают синюю точку.
Идут по дороге друзья-точки, и с каждым днём их становиться всё больше и больше. И наконец, их стало так много, что выстроились они в один ряд плечом к плечу, и получилась линия. Так родилась линия. Когда точки идут прямо, получается прямая линия, когда неровно, криво-линия кривая.
Такое объяснение нового материала в форме составления сказки, детям очень нравится и лучше запоминается новый материал.
Задания на развития беглости.
- Найти несколько возможных решений.
- Выбрать лучший способ решения.
- Установить сходство и различие.
- Определить причинно-следственные связи.
Задания на развития креативности мышления.
- Сформулировать свои вопросы.
- Определить, в чём заключается противоречие, сформулировать и конкретизировать его.
- Высказать свои критические замечания.
- Самостоятельно оценить ответы одноклассников.
- Исправить ошибки.
Можно предложить детям следующие задания:
- Слуховой диктант: 1,3,6, 10, 15…
- Придумай свою числовую закономерность.
- Придумай закономерность из геометрических фигур.
- Изобразите новую геометрическую фигуру, дайте ей название.
- На доске начерчены два неодинаковых отрезка. Придумай прибор, позволяющий сравнить их.
- Начерти прямоугольник с периметром 24 см. (6 решений)
- Найди корень уравнения (х-17)*0=0 (множество чисел от 17 до бесконечности)
- Змей Горыныч обещал детям выпустить их на волю, если они принесут ему воды без самого ведра (дополнительное условие: зимой). Воду можно заморозить.
- Персей убил Медузу Горгону, смотрясь в щит, отполированный до блеска. А каким образом ещё можно решить эту задачу? Ответы детей могут быть разнообразными.
Задания на развитие логического мышления:
- Переформулировать задачу, перевести её с образного, художественного языка на математический.
- Выбрать рациональное решение и довести его до логического окончания.
- Определить, все ли данные задачи использованы при решении задачи.
- Установить, приняты ли во внимание все понятия, содержащиеся в задаче.
Задания, направленные на развитие логического мышления, углубляют математические знания детей, развиваются такие мыслительные операции как анализ и синтез, сравнение, классификация, обобщение.
Можно предложить детям следующие задачи:
- Наглядно-образное мышление.
- развитие мышления у детей, упражнения, задачи. Само понятие образного мышления подразумевает оперирование образами, проведение различных операций (мыслительных) с опорой на представления. Поэтому усилия здесь должны быть сосредоточены на формировании у детей умения создавать в голове различные образы, т. е. визуализировать. Упражнения на формирование подобного умения достаточно подробно описаны в разделе по развитию памяти. Здесь мы их дополним ещё несколькими заданиями на визуализацию.
- Упражнения на визуализацию.
- Упражнение № 1. «На что это похоже?»
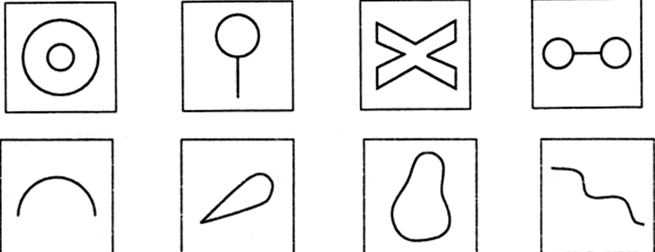
Рис. 1.
- Задание: надо придумать как можно больше ассоциаций на каждую картинку. Оценивается количество и качество (оригинальность) образов. Упражнение хорошо проводить с группой детей в форме соревнования.
- Упражнение № 2. Задание типа «Заполни пробел».
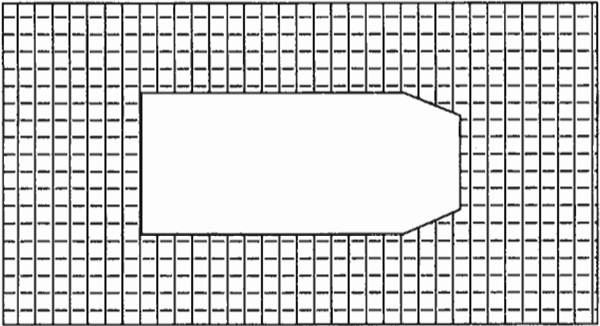
Рис. 2.
- После того, как процесс визуализации достаточно хорошо усвоен детьми, можно переходить к непосредственному оперированию образами, т. е. к решению простейших мыслительных задач с опорой на представления.
- Упражнение № 3. Игра «Кубики». Материал состоит из 27 обычных кубиков, – склеенных между собой так, что получается 7 элементов:
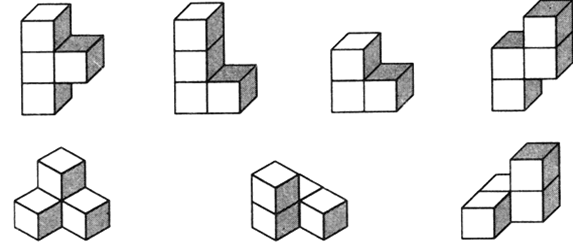
Рис. 3.
Осваивается эта игра поэтапно.
- Первый этап – рассматривание элементов игры и нахождение сходства их с предметами и формами. Например, элемент 1 – буква Т, 2 – буква Г, элемент 3 – уголок, 4 – зигзаг молнии, 5 – вышка со ступеньками, 6 и 7 – крылечко. Чем больше будет найдено ассоциаций, тем лучшее и эффективнее.
- Второй этап – освоение способов присоединения одной части к другой.
- Третий этап – складывание объёмных фигур из всех частей по образцам с указанием составных элементов. Целесообразно проводить работу в следующей последовательности: предложить детям сначала рассмотреть образец, затем расчленить его на составляющие элементы и сложить такую же фигуру.
- Четвертый этап – складывание объёмных фигур по представлению. Вы показываете ребёнку образец, он тщательно его рассматривает, анализирует. Затем образец убирают, а ребёнок должен составить из кубиков ту фигуру, какую он видел. Результат работы сравнивается с образцом

Рис. 4.
В качестве материала для решения мыслительных задач с опорой на образное мышление могут быть использованы и счётные палочки.
Задачи для решения:
- 1. Саша ел яблоко большое и кислое. Коля ел яблоко большое и сладкое. Что в этих яблоках одинаковое? разное?
- 2. Маша и Нина рассматривали картинки. Одна девочка рассматривала картинки в журнале, а другая девочка – в книжке. Где рассматривала картинки Нина, если Маша не рассматривала картинки в журнале?
- 3. Толя и Игорь рисовали. Один мальчик рисовал дом, а другой – ветку с листьями. Что рисовал Толя, если Игорь не рисовал дом?
- 4. Алик, Боря и Вова жили в разных домах. Два дома были в три этажа, один дом был в два этажа. Алик и Боря жили в разных домах, Боря и Вова жили тоже в разных домах. Где жил каждый мальчик?
- 5. Коля, Ваня и Сережа читали книжки. Один мальчик читал о путешествиях, другой - о войне, третий – о спорте. Кто о чем читал, если Коля не читал о войне и о спорте, а Ваня не читал о спорте?
- 6. Зина, Лиза и Лариса вышивали. Одна девочка вышивала листочки, другая – птичек, третья – цветочки. Кто что вышивал, если Лиза не вышивала листочки и птичек, а Зина не вышивала листочки?
- 7. Мальчики Слава, Дима, Петя и Женя сажали плодовые деревья. Кто-то из них сажал яблони, кто-то – груши, кто-то – сливы, кто-то – вишни. Что сажал каждый мальчик, если Дима не сажал сливы, яблони и груши, Петя не сажал груши и яблони, а Слава не сажал яблони?
- 8. Девочки Ася, Таня, Ира и Лариса занимались спортом. Кто-то из них играл в волейбол, кто-то плавал, кто-то бегал, кто-то играл в шахматы. Каким спортом увлекалась каждая девочка, если Ася не играла в волейбол, в шахматы и не бегала, Ира не бегала и не играла в шахматы, а Таня не бегала?
- Эти восемь задач имеют три степени сложности. Задачи 1-3 - самые простые, для их решения достаточно оперировать одним суждением. Задачи 4-6 – второй степени сложности, поскольку при их решении необходимо сопоставить два суждения. Задачи 7 и 8 - самые сложные, т. к. для их решения нужно соотнести три суждения.
- Обычно трудности, возникающие при решении задач с 4 по 8, связаны с невозможностью удержать во внутреннем плане, в представлении все обстоятельства, указанные в тексте, и они путаются, поскольку не пытаются рассудить, а стремятся увидеть, представить правильный ответ. Эффективен в этом случае прием, когда ребенок имеет возможность опираться на наглядные представления, помогающие ему удержать все текстовые обстоятельства.
Нестандартные задачи на умножение и деление
- Можно ли 10 книг расставить на 3 полках поровну?
- Чему равно произведение 0*1*283*4*5?
- Запиши все пары чисел, произведение которых равно 12.
- Хватит ли 8 двухместных парт, чтобы рассадить 20 учеников?
- Придумайте и запишите такое число, не равное 0, которое делится на 3, на 4, на 6.
- Запиши цифру 5. Какую цифру нужно приписать справа, чтобы полученное число разделилось на 6?
- В записи 6 5 2 расставь знаки действия и скобки так, чтобы значение полученного выражения было равно 42. Запишите равенство.
- Каждый торт разделили пополам, а каждую половинку ещё пополам. На каждое из 12 блюдец положили 1 кусок торта. Сколько было тортов?
- Через 5 лет Петя будет вдвое старше, чем сейчас. Сколько лет ему сейчас?
- Какие два целых числа, если их перемножить, дают столько же, сколько получается от их сложения?
- Лена хотела умножить какое-то число на 7. При умножении она ошиблась и у неё получилось18, что на 3 меньше верного ответа. Какое число Лена хотела умножить?
Сказка о том, как прямая превратилась в отрезок
Жил был карандаш. Был он очень любознательный и хотел все знать. Увидит незнакомую линию и непременно спросит:
- Как эта линия называется?
Вышел однажды карандаш на прямую линию и пошел по этой прямой. Шел, шел по прямой линии, долго шел. Устал, остановился и говорит:
- Долго ли я ещё буду идти? Скоро ли конец прямой?
- Засмеялась прямая:
- Эх, ты, карандаш! Ведь ты не дойдёшь до конца. Разве ты не знаешь, что у прямой нет конца?
- Тогда я поверну назад, – сказал карандаш. – Я, наверно, пошёл не в ту сторону.
- И в другую сторону тоже не будет конца. У линии совсем нет концов. Прямая даже спела про себя песенку:
- «Без конца и края
Линия прямая!
Хоть сто лет по ней иди,
Не найти конца пути.»
Опечалился карандаш, узнав, что у линии совсем нет концов.
- Как же быть? Что же мне так и придётся идти без конца?
- Если не хочешь идти без конца, то отметь на прямой две точки, – подсказала прямая.
- Ура! – закричал карандаш. Появились два конца, теперь могу гулять по прямой линии от точки до точки. Что же получилось на прямой? Как это называется?
- Это мой отрезок, – улыбнулась прямая линия.
- Отрезок прямой! Отрезок прямой! – с удовольствием повторял карандаш, прогуливаясь по отрезку от одного конца до другого»
Задания на разминку.
Основной задачей разминки является создание у ребят определенного положительного эмоционального фона, без которого эффективного усвоения знаний невозможно. Поэтому вопросы, которые могут быть включены в разминку, достаточно легкие, способные вызвать интерес, и рассчитаны на сообразительность, быстроту реакции, шуточные. Но они же и подготавливают ребёнка к активной учебной деятельности.
- Какое сегодня число? (1 класс)
- День недели? Месяц?
- Какая буква третья в алфавите?
- Быстро назовите пять имен девочек?
- Сколько всего ушей у трех мышей?
- Росло 4 груши. На каждой – по три ветке, на каждой ветке по три яблока. Сколько всего яблок?
- Сколько яиц можно съесть натощак?
- Одно яйцо варят 4 минуты. Сколько времени надо варить 5 яиц?
- Перечислите пять деревьев, названия которых начинается с гласной буквы?
- Сколько концов у двух палок? А у двух с половиной?
- Кто становится выше, когда садится?
- Стоят два барана. Один смотрит на юг, другой на север. Видят ли они друг друга?
Приведу пример открытых заданий (на которые нет и не может быть заранее известных ответов и решений).
- Что общего и в чем отличие цифр от 1 до 9 и девяти цветных стекол и одного прозрачного?
- Сочини сказку про «+», «-», «=».
- Дай свое определение «уменьшаемому».
- Изобрети новую геометрическую фигуру с 6 вершинами. Дай ей название.
- Сравни таблицу умножения с алфавитом и найди, чем они похожи, а чем отличаются.
- Разработай рекомендации для своих товарищей о том, как быстрее выучить таблицу умножения.
Числовые последовательности
Условия задачи очень простые.
- Взгляни на ряд чисел, отделенных друг от друга запятыми.
- Постарайся понять правило, по которому составлен этот ряд, и попробуй описать это правило словами.
- Догадайся. каким должно быть следующее число.
- Запиши его в конце ряда.
- Проверь решение.
- Если решение правильное, обведи красным карандашом номер примера.
- Посчитай, сколько задач ты решил.
- Если правильно решено больше половины всех задач, поставь себе отметку 5.
- Если ты справился с половиной или с меньшим числом задач, поставь себе отметку 4.
Начнём с самых простых примеров.
- 3, 4, 5, 6, 7, 8________________________________________
- 5, 7, 9, 11, 13________________________________________
- 4, 8, 12, 16, 20_______________________________________
- 11, 22, 33, 44, 55, 66__________________________________
- 29, 39, 49, 59, 69, 79__________________________________
- 87, 75, 63, 51, 39, 27__________________________________
- 112, 223, 334, 445, 556________________________________
- 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, _______________________________
- 100, 99, 97, 94, 90, 85_________________________________
- 10.123, 234, 345, 456, 567, 678__________________________
Различного рода задания способствуют развитию: памяти, внимания, воображения, мышления, но и позволяют углубить знания детей, разнообразить методы и приемы познавательной деятельности.
Предоставляю вашему вниманию разработку креативного урока математики в 3-м классе по теме «Сложение и вычитание трёхзначных чисел в столбик».
Структура креативного урока:
Блок 1: М (мотивация)
Блок 2: СЧ (содержательная часть)
Блок 3: ПР (психологическая разгрузка)
Блок 4: Г (головоломка)
Блок 5: ИР (интелектуальная разминка)
Блок 6: СЧ (содержательная часть)
Блок 7: КИП (компьютерная интеллектуальная поддержка)
Блок 8: Р (резюме)
Цели урока:
Образовательные:
- познакомиться с алгоритмом письменных приёмов сложения и вычитания трёхзначных чисел, аналогичных таким же приёмам при сложении и вычитании двузначных чисел;
- закрепить навык применения алгоритма письменного сложения и вычитания;
- закрепить умение решать составные задачи.
Развивающие:
- развивать навык устного счёта;
- совершенствовать мыслительные операции: анализа, сопоставления;
- развитие умения аргументировать своё мнение;
- развивать интерес детей к математике, их математические способности;
- развитие мыслительной деятельности, познавательной активности, мышления, наблюдательности, внимания, памяти;
- развитие умения давать самооценку своей деятельности;
Воспитательная:
- воспитывать дисциплинированность, ответственность, способность сопереживать, самоуважение; активность, усидчивость, прилежание, любознательность, заинтересованность и пытливость в процессе учения;
- воспитывать взаимопомощь, взаимовыручку;
- воспитание и укрепление интереса к математике;
- создание благоприятного психологического климата для возможности раскрытия потенциала каждого ребёнка.
Оборудование: персональный компьютер с программой PowerPoint, медиа-проектор, интерактивная доска, таблица-алгоритм, сигнальные веера, числовые блокноты, бланк с тестом.
Блок 1. Мотивация
Звенит звонок веселый,
Зовет нас на урок.
Такой порядок в школе,
Не забывай дружок!
Все у парты ровно встали,
Улыбнулись, подравнялись.
Поздоровались с гостями.
Тихо сели за свой стол.
Попрошу вас, ребята, на уроке быть внимательными, работать активно, не бойтесь ошибиться! Помните, что не ошибается только тот, кто ничего не делает.
Блок 2. Содержательная часть
Сообщение темы и целей урока.
Определите тему сегодняшнего урока. Совершенно верно. Тема нашего урока: «Сложение и вычитание трёхзначных чисел в столбик».
Сегодня на уроке нам и предстоит поработать над этим приёмом.
Поставьте перед собой цели.
Работа по теме урока.
Повторение алгоритма письменного сложения и вычитания.
А сможете ли вы самостоятельно объяснить, как сложить эти числа столбиком? (Да, как складывали двузначные числа)
Отработка алгоритма письменного сложения и вычитания.
Устная работа.
Повторим алгоритм сложения в столбик, пользуясь памяткой, который лежит у вас на партах. Выполним сложение в столбик наших числовых выражений.
Назовите 1 слагаемое. 531
Назовите 2 слагаемое. 19
Что помним при записи? (Единицы пишем под единицами, десятки под десятками, сотни под сотнями) Что складываем сначала?
Единицы: 9+1=10, 0 пишем под единицами, 1 десяток запоминаем.
Что складываем затем?
Десятки:3+1+1=5, под десятками пишем 5.
Сотен 5.
Читаю ответ: 550.
Чей ответ был верным? (ничей)
Почему? (Не знали правила)
А вы усвоили?
Проверим, всё ли верно сделали. Помогут нам в этом сигнальные карточки.
На сегодняшнем уроке мы продолжим путешествие по страницам нашего учебника математики. А вместе с нами будут герои повести Н. Носова «Витя Малеев в школе и дома», которые стали для вас уже настоящими друзьями.
Назовите главного героя этой повести (Витя Малеев).
Что вы знаете о нём?
Кто был его лучшим другом? (Костя).
Вот с ними мы и отправимся за новыми знаниями. Вы готовы? Тогда вперёд!
Работа с числовым рядом.
Витя с Костей сразу принялись за дело и быстро справились.
Если правильно решил Костя, вы должны просигналить зелёным цветом, если Витя – синим.
420+80=500 500-60=340
600 440
380+50=530 410-30=380
430 360
Прочитайте 1 выражение. Выражения читайте по-разному. Просигнальте.
Проверим.
Объясните, как вы считали. Какое правило вспомнили?
Трёхзначные числа складываем и вычитаем по разрядам.
Кто считал по-другому?
Далее-аналогично.
Работа в парах.
Молодцы, ребята! Но это ещё не все выражения. Продолжим проверку.
Прочитайте следующее выражение:
426+231=657
675
Найдите значение данного выражения самостоятельно. Работаем в парах!
Помните о правилах работы в парах. Просигнальте, кто же прав. Объясните, как считали.
Значение следующего выражения найдите самостоятельно, также работая в парах.
678-345=233
333
Просигнальте, кто прав
Проверим, всё ли они верно сделали. Помогут нам в этом сигнальные карточки.
Блок 3. Психологическая разгрузка
Физминутка:
Дружно с вами мы считали и про числа рассуждали,
А теперь мы дружно встали, свои косточки размяли.
На счет раз кулак сожмем, на счет два в локтях сожмем.
На счет три – прижмем к плечам, на 4 – к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем – добрыми всегда мы будем.
На счет шесть прошу всех сесть.
Числа, я, и вы, друзья, вместе дружная 7-я.
Блок 4. Головоломка
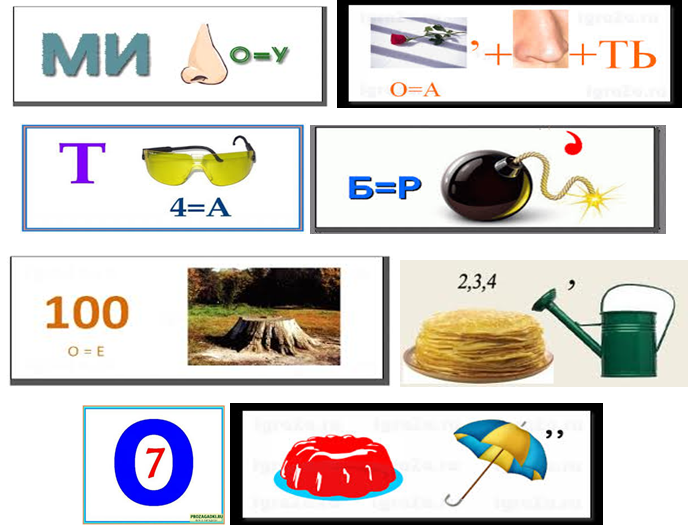
Рис. 5.
Блок 5. Интеллектуальная разминка
Задача 1. Ребята измеряли шагами длину игровой площадки. У Лизы получилось 25 шагов, у Полины – 27, у Максима – 22, а у Юры – 24. У кого из ребят самый короткий шаг? (У Полины)
Задача 2. На часах было 11:45, когда начался мультфильм. Он длился 50 минут. Точно в середине просмотра пришла мама и позвала обедать. Какое время показывали часы в этот момент? (12:10)
Задача 3. Четыре девочки ели конфеты. Аня съела больше, чем Юля. Ира – больше, чем Света, но меньше, чем Юля. Расставь имена девочек в порядке возрастания количества съеденных конфет. (Света, Ира, Юля, Аня)
Задача 4. У сороконожки 90 ножек. Она купила 13 пар сапожек. Но при этом 16 ног остались босыми. Сколько пар старых сапожек было на сороконожке до покупки новых сапожек? (24)
Задача 5. Петя и Коля живут в одном многоэтажном доме. Квартира Коли на 12 этажей выше, чем Пети. Вечером Петя поднимался по лестнице к Коле. Когда он прошёл половину пути, то оказался на 8 этаже. На каких этажах квартиры мальчиков? (П-2, К-14)
Блок 6. Содержательная часть
Пока мы с вами разминались, Витя с Костей получили задание от Ольги Николаевны, их учительницы: найти значения математических выражений с числами из нашего числового ряда.
А теперь применим алгоритм на практике. Работаем в тетради. Стр. 58, сначала прочитаем сведения на странице, а затем выполняем № 2. Используйте таблицу-алгоритм.
Ну что же я думаю, что и ребята, и вы усвоили этот алгоритм.
Самостоятельная работа (тест).
На следующий день Костя и Витя пришли в школу. А там мальчиков и их одноклассников ожидала самостоятельная работа. (детям раздаются тесты)
Проверьте, правильно ли школьники выполнили задание и занесите результаты вашей проверки в таблицу.
Взаимопроверка.
(Ответы на слайде). ( - + - + - )
Решение задачи.
Не успел Витя прийти домой и передохнуть, как подходит к нему Лика, это младшая сестра Вити, и говорит: «Помоги решить задачу.»
Как вы думаете, сможет ли Витя помочь сестре?
А вы решите эту задачу? (Стр. 58 № 3)
Разбор задачи.
Прочитайте задачу. Что нам известно в задаче? Прочитайте вопрос задачи.
Составим краткую запись.
План решения.
Проверка: ученик у доски объясняет решение задачи.
Так ли у вас? 156 – 30 = 126 (д садов)
156 + 126 = 282 ( всего)
Что помогло Вите решить задачу? (Внимание, трудолюбие).
Блок 7. Компьютерная интеллектуальная поддержка
С помощью компьютерной программы решите ещё одну задачу:
Блок 8. Резюме
Приём рефлексии:
Пришла пора подвести итоги. Какой приём мы повторяли на уроке? Расскажите алгоритм письменного сложения и вычитания трёхзначных чисел. Посмотрите на слайд и оцените свою работу на уроке. Я довольна вашей работой на уроке.
Дома вам предстоит решить задачу и найти значение выражений столбиком. Уровень сложности вы выберите самостоятельно, ориентируясь на цвет.
А оценка всему классу: МОЛОДЦЫ! УРОК ОКОНЧЕН!
Систематическая работа учителя в режиме творческого обучения, когда ежедневно ученикам на уроках предлагается решать нестандартные задания, способствует формированию положительного отношения к заданиям проблемно-поискового характера, гибкости мышления, умению проводить мини-исследования, содействует проявлению более высокой степени самостоятельности в постановке вопросов и поиске решений.
Таким образом, развивая творческое (креативное) мышление мы можем добиться хороших результатов в обучении и развитии ребёнка.
Ссылки на источники
- Бухвалов В. А. Алгоритмы активизации творческого мышления // Школьный психолог. – 2004. – № 4. – С. 27.
- Утёмов В. В. Учебные задачи открытого типа // Концепт: научно-методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв». – Май 2012, ART 1257. – Киров, 2012 г. – URL: http://www.covenok.ru/koncept/2012/1257.htm.
- Утёмов В. В. Задачи открытого типа как средство развития креативности учащихся средней школы // Концепт: научно-методический электронный журнал официального сайта эвристических олимпиад «Совёнок» и «Прорыв». – Декабрь 2011, ART 1102. – Киров, 2011 г. – URL: http://www.covenok.ru/ koncept/2011/1102.htm.
- Утёмов В. В. Развитие креативности учащихся основной школы: Решая задачи открытого типа. – Saarbrucken: LAP LAMBERT Academic Publishing GmbH & Co. KG (Germany), 2012. – 186 с.
- Савазева, В. Ю. Решение творческих задач как условие развития креативного мышления / Начальная школа. Плюс до и после. – 2004. – №7. – с. 31–37.
