Нестандартные уроки – средство активизации познавательной деятельности учащихся

Современная жизнь диктует свои условия, а именно, необходимость формирования творчески активной личности, обладающей способностью эффективно и нестандартно решать новые жизненные проблемы. Воспитание креативной личности одна из наиболее сложных и интересных задач современной педагогики. Помощником в решении этих задач может служить инновационная педагогическая система НФТМ-ТРИЗ профессора М. Зиновкиной – система непрерывного формирования творческого мышления и развития творческих способностей обучаемых с активным использованием теории решения избирательских задач [1, 2].

Ученик всё ещё на учебных занятиях бывает лишь пассивным созерцателем и слушателем урока. Главное место на нём отводится нередко монологу учителя. Так называемый устный опрос отдельных учащихся так же не вызывает особой активности остальных учеников класса.

Стержневая идея – это побуждение учащихся к активизации познавательных сил, самостоятельному творчеству на каждом уроке, к реализации скрытых возможностей каждого отдельного школьника. При такой постановке обучения ученики много думают и делают, никогда не скучают и не ждут звонка с урока. Они захвачены, увлечены и сосредоточены.

Существует много путей реализации подходов в обучении. Один из них – изменение традиционной структуры урока. При традиционной структуры урока 45 минут делятся на несколько частей – проверка домашнего задания, объяснение нового материала, закрепление его. Вместо суетливой спешки на уроке, в попытках охватить все его стороны, используется система совместной работы учащихся и учителя, включающая себя:

• Урок – лекция.

 Это совместное размышление и деятельность учителя и учеников. Его необходимо подготовить и провести, таким образом, чтобы целая тема был рассмотрена крупным блоком и обеспечены высокий научный уровень изучаемого материала, а также доступность изложения. Во время лекции рассказ учителя сочетается с вопросами к классу, с приглашением к сотворчеству, размышлениям. Важно чтобы учитель не просто констатировал понимание или непонимание, а побуждал школьников к тому, чтобы они открыто говорили, где и в чём испытывают трудности при усвоении учебного материала. Урок требует большой подготовки и учителю приходится выступать в роли информатора при этом не забывая держать в поле зрения каждого ученика. Сложность урока определяется и тем обстоятельством, что в ходе этого занятия необходимо заинтересовать учащихся, добиться понимания сути изучаемого вопроса, познакомить учеников с методами математических исследований, заложить основы для доступной исследовательской деятельности.

• Урок – консультация.

Урок организован таким образом, что учащиеся вынуждены задавать вопросы, делиться своими трудностями непосредственно на уроке. После изучения параграфа или какой – то его части проводится урок- консультация. Заранее ученики получают домашнее задание – подготовить карточки с условиями задач по теме, которые они не могли решить или решение которых их интересует. Такое задание не бывает неожиданным. Ученикам заранее известен срок консультации. Учитель постоянно входе изучения темы побуждает их к поиску и отбору наиболее интересных задач. Проведение уроков-консультаций, что сначала, что ученики не представляют себе какие задачи нужно включить в карточки. Совместная деятельность учителя и учащихся по подготовке к уроку-консультации постепенно приводит к тому, что учитель перед уроком получает от учащихся карточки с таким числом задач, которые невозможно решить за один урок. Поэтому выбираются несколько из них, чтобы решение минимального числа задач вооружило бы всех школьников приёмами отыскания решений сформулированных ими задач. Такие уроки высоко ценятся учащимися, так как на них рассматриваются не подготовленные задачи, а такие, решение которых рождается на их глазах и пр.и активном участии всего класса. Ниже в статье приведён фрагмент такого урока (Урок геометрии в 7 классе).

• Урок-зачёт

На таком уроке сочетаются индивидуальные, коллективные и групповые формы работы.

Структура урока:

• Разминка 5-7 минут;
• Опрос ассистентов первой группы без подготовки (10-12 минут);
• Опрос ассистентов второй группы ассистентами первой группы;
• Первая группа ассистентов решает задачи до конца урока;
• Вторая группа ассистентов ведет опрос. Ответившие на «4» и «5» присоединяются ко второй группе ассистентов.

К зачёту каждый ученик заготавливает лист учета знаний, в котором будут выставлены оценки за определенный вид деятельности.

Лист учёта__________________________
Вид деятельности	Оценка
Теория без доказательства
Решение устных задач
Теория с доказательством
Решение задач
Итоговая оценка

• Зачёт-практикум

Проводится по тем разделам, где мало теоретических вопросов. Урок начинается с разминки: решение устных задач, каждая задача – 2 балла. Листки с ответами сдаются учителю. Затем каждый ученик получает билет с задачами различной трудности, каждая задача оценена определенным количеством баллов в зависимости от трудности. Задачи решаются на отдельных листах, чтобы избежать списывания. Подведение итогов: до 10 баллов – «2»; 10-15 баллов – «3»; 16-19 баллов – «4»; 20-29 баллов – «5». В конце урока вывешиваются решения задач, разбираются ошибки.

• Урок-конференция

Весь класс разбивается на группы по интересам. Распределяются темы докладов, формулируется цель дискуссии. Члены группы готовят выступление по теме и их наглядную иллюстрацию (чертежи, плакаты, презентации и т.д.). Поставленные вопросы должны освещаться глубоко, вызывать интерес у учащихся. Докладчиков должно быть более 3 человек. Требуется, чтобы они говорили правильно, выразительно, приводили доказательства. К учебной конференции прибегают тогда, когда предполагается изучать легкий, но объёмный материал, хорошо изложенный в разных пособиях. После докладчика выступают оппоненты. Основной метод обучения – дискуссия, в ходе которой разбирается учебный материал. Учитель направляет ход дискуссии, формирует основные вопросы, ориентирует учащихся на их обсуждение. В заключении подводится итог конференции.

• Семинар

Семинар проводится с целью совершенствования и закрепления знаний.

• организационный;
• постановка цели;
• актуализация знаний;
• выдвижение проблем, их обсуждение;
• обобщение и систематизация знаний;
• определение и разъяснение домашнего задания.

Семинар предполагает интенсивную предварительную работу с учебниками, пособиями, книгами. В ходе семинара формулируются проблемы, которые решают ученики, находя свои способы доказательства. Семинарские занятия проводятся с учениками старших классов, которые владеют навыками работы с литературой.

 

• Урок – пресс-конференция

Такой урок лучше проводить как заключительный по изучаемой теме. Как правило, он проводится в виде ролевой игры, т. к. предполагает наличие определенных ролей: это беседы членов делегаций или других групп с представителями телевидения, прессы, журналистами газет и журналов, фотокорреспондентами. Перед участниками конференции ставится речевая задача. В ходе урока учащиеся тренируются в монологической речи, в умении задавать проблемные вопросы дискуссионного характера, аргументировано отвечать на вопросы. Детям нравятся такие уроки, т. к. они предполагают развитие навыков самостоятельной работы, стремление к творческому поиску.

• Урок – соревнование.

 Используется прием моделирования, много игровых моментов, соревнования, которые повышают познавательную активность и стимулируют детей.

Класс делится на команды. Получив тему и вопросы, капитаны команд готовят свои группы к состязанию: прежде всего, выясняет все ли прочитали теоретический материал.

Команды обдумывают, обсуждают вопросы. Капитаны обращаются за консультацией к учителю. Если вопрос трудный, то можно немного подсказать, но учитель просит капитанов не раскрывать «тайну», чтобы дать учащимся подумать. Готовит ответ на вопрос вся команда. Мнение общее, а выражает – его кто-то один. Команды, ответы которой самые полные, точные, аргументированные получают самые высокие оценки.

За каждое правильно и быстро выполненное задание командам выдаются жетоны. В конце урока считают жетоны. Дух соревнования оказывает влияние на всех. Здесь же корректируется речевая деятельность отдельных учеников, если она не согласуется с общим мнением команды.

• Уроки фантазии
• Уроки - путешествия

Уроки-сказки обычно проводятся после изучения темы для отработки навыков решения, для закрепления изучаемого материала. Игра проводится на основе сказки. Класс разбивается на 2-3 команды. Начинается рассказ, ставится проблема, учащиеся, применяя необходимые знания, решают ее. Учитывается скорость и правильность решения. В конце урока подводятся итоги всей игры. Устанавливается команда – победитель, часть учеников получает оценки. Такую форму урока чаще всего используют в 5 классе. Но иногда она приемлема и в более старших классах.

Урок-путешествие – это одна из наиболее часто используемых форм проведения уроков в 5-7 классах. Как и все дидактические игры, «путешествие» проводится после изучения темы, для отработки умений и навыков, закрепления и обобщения изученного материала. Класс делится на несколько групп. «Путешествуем» по «остановкам» или «станциям», на каждой из которых команды получают задание, а иногда – оценки. В группах выделяются помощники, которые заполняют специальные ведомости. В конце «путешествия», учитывая записи в ведомостях, оценивается каждый ученик.

• Уроки общения

Устный журнал не требует соревнования. Важно само участие в выпуске журнала. Во время проведения урока нужно дать слово как можно большему числу учеников. Учащиеся заранее читают математическую литературу, находят в ней интересные факты, которые излагают за 1-2 минуты. Ведущие готовят ряд коротких рассказов об истории математики из тех разделов, которые не издаются в школе, но доступны учащимся. Цель ведущих – изложить свои заготовки, увлечь беседой учащихся. Они говорят таинственно, весело, обыгрывают сообщаемый факт, как эстрадную миниатюру.

Игра направлена на повышение активности учащихся в процессе усвоения новых знаний. Формулируется учебная проблема, а учащиеся должны решить ее. Они понимают, что для решения проблемы недостаточно имеющихся знаний. Каждая команда имеет право задать минимальное число вопросов с тем, чтобы извлечь из ответов максимум информации. В игре учитель как бы не желает выдавать информацию, а ученики поставленными вопросами принуждают его к этому. И если в диалоге при минимальном количестве вопросов у какого-нибудь ученика наступает озарение, то задача по развитию творческого мышления учащихся выполнена .

• Урок-КВН

План проведения:

• Разминка. Самостоятельная пятиминутная работа по обязательным результатам обучения (можно использовать тестовые задания).
• Блицтурнир. Предлагаются задания типа «Что бы это значило», «Найди ошибку».
• Конкурс «Домашнее задание».
• Конкурс капитанов. Капитан решает задания на доске, учащиеся команды – на своих местах, при необходимости команда может помочь капитану.
• Конкурс консультантов. Каждый консультант получает задание, решает его на доске и объясняет решение. Задача соперников – завалить консультантов, разыграв непонимание.
• Подведение итогов.

Конечно же, этот план носит приблизительный характер.

• Урок без темы.

Данный урок состоит следующих этапов.В начале урока зачитывается фрагмент литературного произведения, в котором звучит философский вопрос. Например, «Алиса в стране чудес» Л. Кэррол. «В нескольких шагах от неё сидел на ветке Чеширский кот.

- Скажите, пожалуйста, куда мне отсюда идти?

- А куда ты хочешь попасть?- ответил Кот.

- Мне всё равно…- сказала Алиса.

- Тогда всё равно , куда и идти,- заметил Кот».

О чем хочет поведать этими словами Кот Алисе и зачем они зачитаны?

Рассмотрим фрагмент урока в 5 классе. Этот урок учит наблюдать, наблюдать - это просто замечать. Это умение необходимо любому человеку. Нужно постараться мысленно, а иногда и вслух, начинать свой ответ со слов: «А вот я заметил…». Далее следует этап устной работы над примерами. Учащиеся делятся на пары и со своим напарником обсуждают ход решения. Когда всё готово, поднимают руку.

Далее следует разбор решения примеров.

Следующий этап – это работа над проблемной ситуацией. Например, Нарисовать квадрат 4х4 клетки. Заштриховать его половину; далее ещё одну четверть, далее ещё одну шестнадцатую. Штриховать нужно каждый раз другим цветом.

Посмотрите на рисунок и дайте ответ в следующих примерах:

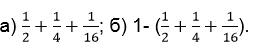
Следующий этап - решение уравнений с обыкновенными дробями и т.д. на усмотрение учителя.

На уроке предлагались задания , на выполнение которых был организован поиск наиболее коротких и экономных путей. А это формирует положительный мотивы учения. Урок не содержит материала, которым обязательно должен овладеть каждый ребёнок. Он появился как бы случайно, направлен в единое русло – наблюдать и решать, решать и наблюдать. Хочешь слушай, хочешь нет. Хочешь запоминай, хочешь нет. Но это свобода видимая. На самом деле последовательность упражнений цепко держит ребят и не выпускает из рук. Таким образом, обеспечивается интенсивная мыслительная деятельность. На этом уроке реализованы идеи: занимательного, нетрадиционного начала урока, постановка целей для того чтобы включить послепроизвольное внимание, опора на наглядность, посильные трудности и необязательность то, что будет на уроке.

• Урок – творчество.

Развитие у школьников творческого мышления одна из важнейших задач в сегодняшней школе. Самостоятельное приобретение учащимися новых знаний – творческий процесс. Большую помощь при этом оказывает введение в обучение творческих заданий. Здесь мы предлагаем творческие задания по геометрии для 7 класса, с помощью которых можно изгнать с уроков скуку и равнодушие. При этом мы помним, что создание положительных эмоций у школьников – мощный инструмент их обучения и воспитания.

1. На первых уроках геометрии семиклассники знакомятся с различными простейшими фигурами, их отношениями, появляется новая терминология, которая нелегко усваивается ими. В связи с этим в устные упражнения каждого урока геометрии включаем следующие задания: опишите рисунок (проецируем на экран рис.1) 

.D

 

.A .B .C a

 

.L .M рис.1

 

Дана прямая a.

Её можно назвать AB, BC, AC.

Даны шесть точек A,B,C,D,L,M

Что можно сказать о их взаимном расположении?

В описании рисунка по очереди вовлекаются все учащиеся класса. От урока к уроку рисунки усложняются.

Замечаем что математическая речь учащихся получает своё развитие, но в основном за счёт классных упражнений. Учебник геометрии ещё не стал для них помощником и консультантом. Вот тут и появляется идея о проведении первой творческой домашней работы по геометрии.

Предлагаем ученикам самим придуматьрисунок и описать его. Обращаем внимание, что хорошим советчиком при выполнении задания может стать, например, учебник. Таким образом, уже с первых уроков геометрии формируем умение работать с книгой, с учебником или с другими источниками информации.

При выполнении задания ученики не ограничены жёсткими временными рамками. Несомненно, этот факт положительно влияет в целом на качество работы. Более того, если ученик получает оценку, которая его не удовлетворяет, то он имеет право вновь вернуться к заданию.

Интересные работы зачитываем в классе, комплектуем выставку лучших сочинений, оригинальных рисунков. На родительских собраниях можно ознакомить родителей с материалами данной выставки.

Опыт показывает, что такая творческая работа оценивается очень высоко. А если учесть, что ученики получают практически первую (хорошую!) оценку по геометрии, то, безусловно, полностью снимается дискомфорт, который часто образуется у учащихся при переходе к систематическому изучению курса геометрии

2. Одним из трудных методов доказательства, с которым ученики встречаются при изучении геометрии, - доказательство методом от противного. Известный советский дидакт М. А. Данилов сделал вывод, что главной движущей силой процесса обучения являются противоречия. Противоречие в условии задачи – главное требование к открытой задаче.

Ученикам предлагается творческое задание: проиллюстрировать применение доказательства методом от противного на примерах из жизни, художественной литературы, из различных школьных учебников.

Здесь могут быть неординарные примеры из курсов биологии, физики, литературы. Данная работа может быть оценена и другими учителями – предметниками.

3. Признаки равенства треугольников - основной рабочий аппарат для дальнейшего изучения геометрии и решения задач. Следовательно, необходимо , чтобы знания учащихся по это теме были глубокими, прочными, осознанными.

С этой целью по окончании изучения признаков равенства треугольников учащимся предлагается следующее творческое задание синтетического характера: составить и решить задачу на применение определений и теорем темы «Равенство треугольников». Общеизвестно, что самостоятельно составленная и решённая задача запоминается лучше, чем просто решённая.

Однако, самостоятельное решение задачи требует от учащихся особых умений. Поэтому при решении задач данной темы мы обращаем внимание учеников на способ составления той или иной задачи. Например, равенство углов вуалируется или в их общности, или в видах углов (вертикальные, смежные равным углам), или в равенствах других пар треугольников и т.д.

Задание ученики выполнили по-разному. Условно их можно разделить на четыре группы.

Так, слабые ученики ограничились лишь тем, что в условии ранее решённой задачи менялись обозначения.

Другая группа – составила задания с переопределённым условием.

Третья группа предложила интересную задачу, но выбрала не рациональный способ решения, надуманный, в погоне за количеством применённых геометрических фактов.

У четвёртой группы ребят были оригинальные задачи и рациональные способы решения. Такие задачи предлагались на последующих уроках. Решение задач, авторами которых были сами ребята, вызвало живой интерес. По окончании урока некоторые учащиеся изъявили желание усовершенствовать свою задачу, чтобы и их фамилия, как автора, прозвучала в дальнейшем. Например, вот такая задача (рис.2)
                                                                 

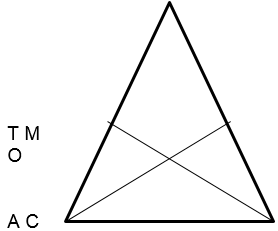
Дано: АВС, АВ = ВС, ВТ = ВМ.

Доказать: АОС – равнобедренный.

При обсуждении задачи ученики открыли различные способы её решения, о которых не подозревал сам автор.

Нестандартные уроки – это всегда уроки-праздники, когда активны все учащиеся, каждый имеет возможность проявить себя, класс становится творческим коллективом. Но слишком частое обращение к нетрадиционным формам организации учебного процесса нецелесообразно, так как приводит к потере устойчивого интереса к предмету. Нетрадиционному уроку должна предшествовать тщательная подготовка, разработка системы конкретных целей обучения.
В новом тысячелетии мы вступили в эпоху, которую в противовес уходящей «индустриальной эпохе» называют «информационной эпохой». Это означает, что самым важным продуктом становится информация. При обмене информацией очень большую помощь оказывают компьютеры. Они позволяют учителю контролировать и степень усвоения материала учеником, и скорость его изложения для каждого конкретного ученика, в зависимости от уровня подготовки. Уже само применение компьютерной техники на уроках позволяет сделать каждый урок нетрадиционным, ярким, насыщенным.