Урок алгебры в 8 – м классе по теме: «Решение уравнений, сводящихся к квадратным»

Этапы урока

Содержание урока

I Оргмомент.

Проверка домашнего задания. (учащиеся тетради с д/з сдают на проверку до начала урока)

 II  Устная работа

III         Новое.         

Связь с устной работой.

№ 2

 На обороте доски заранее подготовлен текст

Знаете ли Вы?  

Пауза

Связь с устной работой.

№3, №4

 Работа с магнитной доской

IV Закрепление.

 VI

Записать на обороте доски

VII Домашнее задание.

VIII 

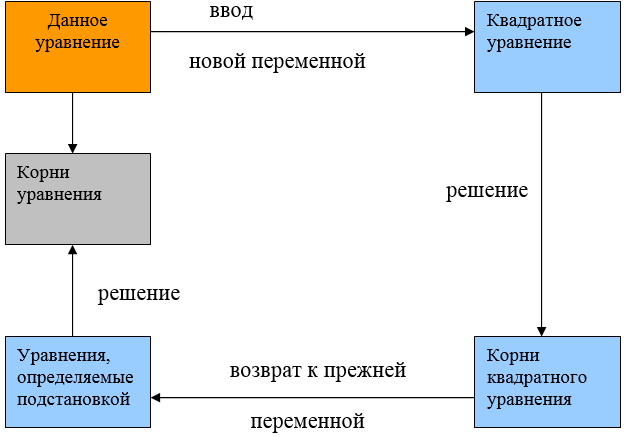
Сегодня на уроке мне хотелось бы вас пригласить «поглубже» заглянуть в замечательный мир математики – в мир уравнений, в мир поиска и исследований.
Но для начала давайте вспомним: 

Какое уравнение называется квадратным?
Какие квадратные уравнения называются неполными?
Приведите примеры неполных квадратных уравнений.                           
Сформулируйте определение дискриминанта квадратного уравнения.
Сколько корней может иметь квадратное уравнение?
Напишите основную формулу корней квадратного уравнения. 
Напишите дополнительную формулу корней квадратного уравнения.
Сформулируйте теорему Виета.                                        
Сформулируйте теорему обратную теореме Виета.                                                                                                        

Все способы решений, известных вам уравнений, можно образно представить в виде “ключей”.

 Символ урока – связка ключей -  «Квадратные уравнения», «Дробно-рациональные уравнения», «Уравнения, сводящиеся  к квадратным».

Задание: Определите вид каждого уравнения и найдите корни          
(№ 1 - № 5), где это возможно выполнить (устно).

На доске записаны уравнения.

1) (ответ:)

2)  (ответ: t₁ = 1, t₂ = 4)

3)  (ответ:)

4)  (D<0, уравнение корней не имеет)

5) (ответ: )

6)

7)

Но в нашей связке есть ещё один "ключик", который вам ещё не известен - «Уравнения, сводящиеся  к квадратным».

И наша задача состоит в том, чтобы «отточить» этот ключик и научиться, таким ключом, открывать тайну уравнений.

Поэтому, тема нашего урока: «Уравнения, сводящиеся  к квадратным».

Давайте рассмотрим уравнение (№ 6).

- Какую особенность в данном уравнении Вы заметили?                         
- Выражение обозначим буквойt. Что изменилось в уравнении? (получилось квадратное уравнение относительно t).                              
И такой подход к решению уравнений называют – методом введения новой переменной, который позволяет свести данное уравнение  к квадратному.

Введем  замену: Пусть  х-1 = t, тогда исходное уравнение примет вид – по т. Виета найдём корни уравнения: t₁ = 1, t₂ = 4.             Но нам нужны значения х.                                                             Вернемся к подстановке: х-1 = t ,получим линейные уравнения:

х-1 = 1                                х-1 = 4

х = 2                                    х = 5

Ответ:

Давайте ещё раз проанализируем решение данного уравнения, каких целей добились.

План исследования уравнения:

1. Провести анализ уравнения.
2. Составить план решения.
3. Реализовать план решения.
4. Составить анализ метода решения и систематизировать опыт.

4 пункт плана исследования уравнения - составление анализа метода решения - это ещё один этап нашей исследовательской работы.

Знаете ли вы, что английский математик Джеймс Джозеф Сильвестр  называл музыку математикой чувств, а математику – музыкой разума.

Релаксация: учащиеся закрывают глаза и расслабляются.           
(Звучит музыка) – 1минута.

Продолжим нашу работу.

Рассмотрим следующее уравнение (№ 7).

Раскроем  скобки, объединяя  1 – 4  множители и 2 – 3 множители. Получим уравнение  
Нетрудно заметить, что если решать уравнение, раскрывая скобки дальше, то в левой части уравнения получится многочлен четвёртой степени – сложно.

Введем замену: Пусть, тогда исходное уравнение примет вид:

Вернемся к подстановке, получим уравнения:

Ответ:

Подведём итог нашей исследовательской работы.                       
Вывод: Итак, два различных  уравнения мы решили одним и тем же методом – методом введения новой переменной, где первоначальное уравнение приводится к квадратному. А теперь давайте попробуем составить алгоритм решения (выполняем четвертый пункт схемы исследования). 
                                       

(У каждого учащегося на столе задание с "алгоритмом" решения).

(Беглый устный разбор).

     а) Какую подстановку можно выполнить в каждом уравнении?

А.                                           

В.

Ответ: у = -2; -1; 0.

     С.  

     D.

Алгоритм.                                                                                         Карточка - практикум. Решите уравнения:                                                                                                                           

Рефлексия.                                                                                            Сегодня на уроке мы только попробовали подобрать наш "ключик" к решению уравнений. Вам предстоит ещё большая работа, чтобы этот ключ работал в совершенстве. Благодарю вас за урок. Желаю удачи вам, новых поисков и открытий. До свидания.