Цели урока:
- совершенствовать навыки работы в Excel при построении и редактировании графиков функций;
- научиться исследовать тригонометрические функции с использованием технических средств;
- научить применять преобразования графиков элементарных тригонометрических функций для построения графиков более сложных функций.
Задачи урока:
Обучающие:актуализация метапредметных знаний, обобщение и систематизация знаний, умений и навыков, полученных учащимися при изучении графических возможностей MS Excel.
Развивающие:
- развивать универсальные общеучебные компетенции (обобщение и анализ информации);
- развивать самостоятельность в приобретении знаний;
- развивать исследовательские и творческие способности;
- развивать умение осознанно воспринимать новый материал;
- развивать умение видеть проблему, анализировать ситуацию, находить пути решения проблемы;
- умение анализировать результаты своей деятельности, сравнивать, сопоставлять, делать выводы, находить рациональные пути;
- умение применять свои знания в различных ситуациях (в том числе нестандартных);
- коммуникативные умения, умения делового общения.
Воспитательные:
- мотивация информационно-технологического творчества учащихся;
- формирование навыков группового поиска и принятия решения;
- развитие способности к саморегулированию и самоуправлению.
Образовательные технологии:
- проблемный диалог,
- работа в группах.
Тип урока: интегрированный урок-практикум.
Оборудование урока:
- Компьютеры с ОС MS Windows XP;
- Приложение MS Windows – MS Excel;
- Интерактивная доска;
- Карточки-задания для домашней работы.
Ход урока
|
Этап урока |
Деятельность учителя |
Деятельность учащихся |
|
1.Организационный (3 мин.) Подготовка учащихся к работе на уроке |
Обращает внимание учеников на сделанные на доске записи (число, тема), ставит цели и задачи урока, задает настрой на отличную работу на уроке, делит учащихся с помощью жребия на две группы. |
Внимательны, заинтересованы в проведении урока, психологически готовы, имеют конспекты. |
|
2. Актуализация опорных знаний (10 мин.)
|
Как вы думаете, в чем необходимость графического представления числовых данных?
Для более наглядного представления и использования в работе на уроках математики графиков элементарных тригонометрических функций у=cos(x) и y=sin(x) мы научились строить эти графики в Excel. Кратко вспомните, как мы это выполняли. Какие знания, полученные на уроках математики нам понадобятся?
|
В любой сфере деятельности существует множество задач, в которых исходные данные и результаты должны быть представлены в графической форме. Умение наглядно представлять информацию в виде графиков и диаграмм – неотъемлемая часть современного образования. При решении различных задач, подготовке отчетов по различным предметам, выполнении заданий нередко возникает необходимость графического представления числовых данных. Основное достоинство такого представления – наглядность. Электронные таблицы предоставляют большой набор возможностей по графическому представлению данных в виде диаграмм и графиков.
Построение графика разбивается на два этапа: - создание таблицы в Excel, состоящей из наборов (x, y) для всех значений х на выбранном интервале (рис.1), - построение диаграммы вида «Точечная» или «График» по полученным данным. (рис.2) |
Рис.1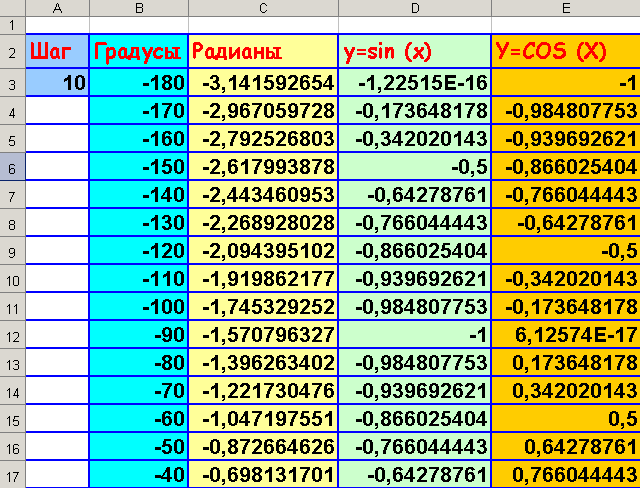
Рис.2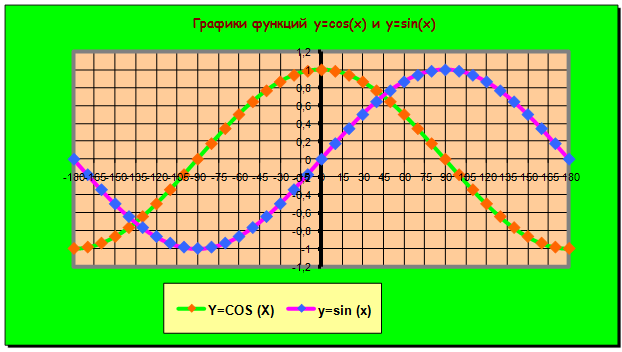
Этап урока |
Деятельность учителя |
Деятельность учащихся |
|
3.Теоретическая часть (13 мин.) Определение проблемы и необходимость в ней разобраться |
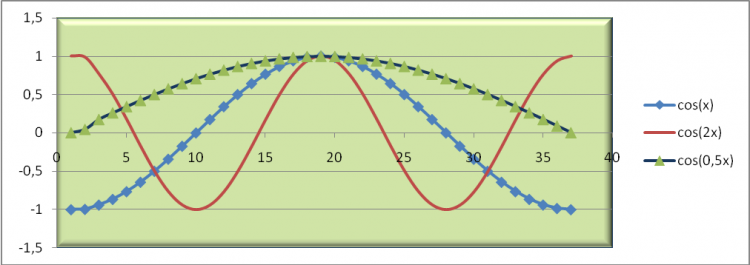
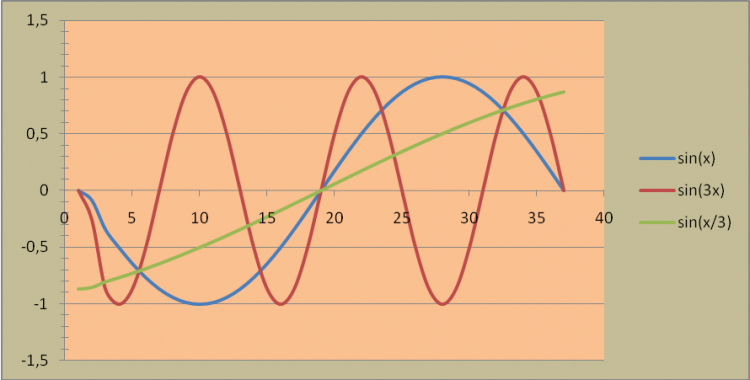
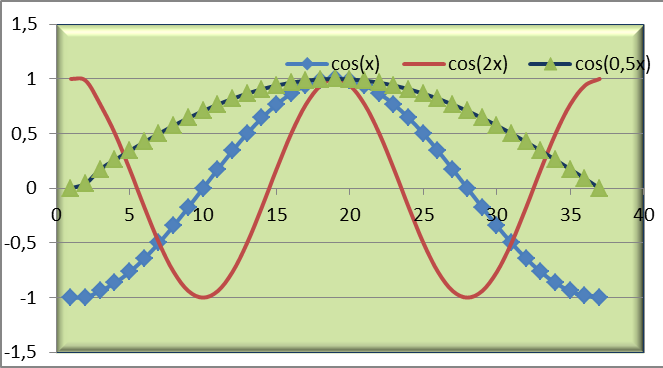
На уроке математики вы проанализировали графики и выяснили, как меняется функция (сжимается, растягивается, сдвигается и т.п.) в зависимости от вводимых коэффициентов: y1=cos (x) y1=sin (x) y2=cos (2x) y2=sin (3x) y3=cos (x/2) y3=sin (x/3). Определили ее свойства (область значений, четность, нечетность, периодичность). А как в MS Excel построить и исследовать изменение свойств этих функций? Организует обсуждение, помогает выбрать оптимальный способ решения. |
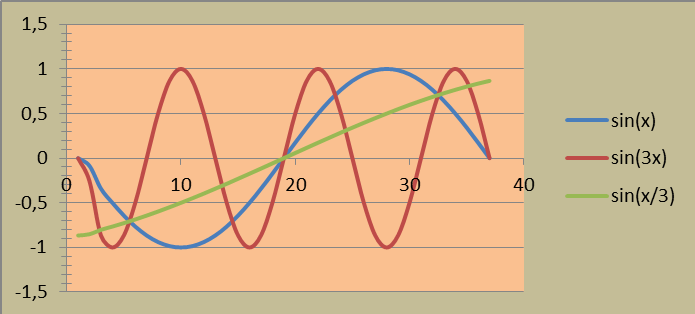
Уточняют информацию. Осуществляют планирование работы в группах. Консультируются с учителем. Учащиеся предлагают разные способы построения графиков тригонометрических функций в электронных таблицах. Группа учащихся №1 демонстрирует и объясняет по Рис.3 как были построены графики (приложение 1) и исследует функции: cos(2x): сжимается вдоль оси X в 2 раза, период π, четная, ОДЗ: -1≤Y≤+1; cos(x/2): растягивается вдоль оси X в 2 раза, период 4π, четная, ОДЗ: -1≤Y≤+1. - группа учащихся №2 демонстрирует и объясняет по Рис.4 как были построены графики (приложение 1) и исследует функции: sin(3x): сжимается вдоль оси X в 3 раза, период 2/3π, нечетная, ОДЗ: -1≤Y≤+1. sin(x/3): растягивается вдоль оси X в 3 раза, период 6π, нечетная, ОДЗ: -1≤Y≤+1. |
|
Этап урока |
Деятельность учителя |
Деятельность учащихся |
|
4.Практическая часть Поиск решения (открытие нового знания), формулирование правила (9 мин.) |
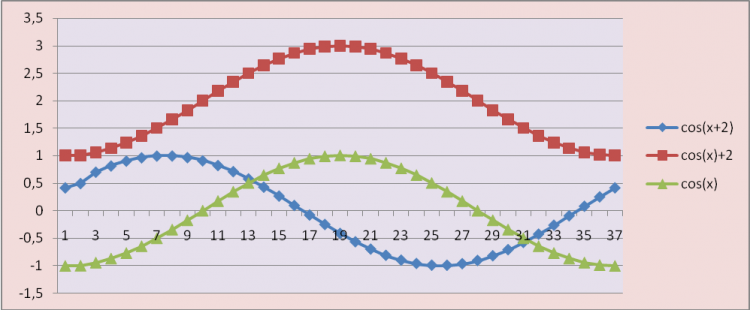
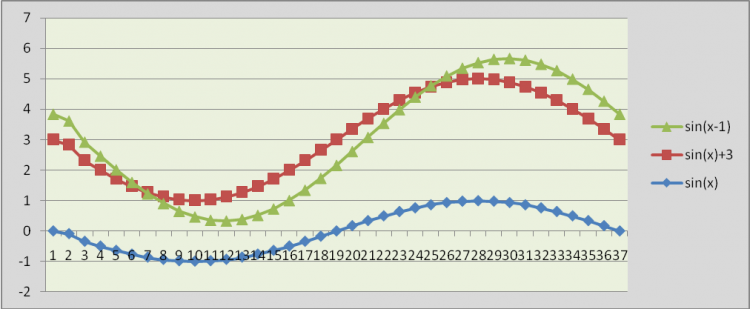
Постановка исследовательской задачи Задание 1. Произвести расчет и построить графики функций на отдельных диаграммах на интервале [-2π; 2π] с шагом 10 y1=cos (x) y1=sin (x) y2=cos (x) +2 y2=sin (x) +3 y3=cos (x+2) y3=sin (x-1)
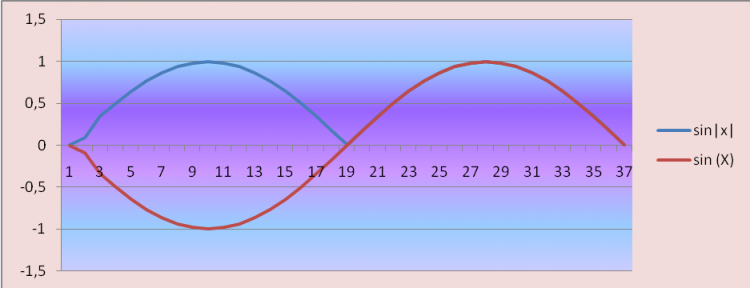
Задание 2 (учитель выполняет вместе с учащимися). Произвести расчет и построить графики функций на отдельных диаграммах: y1=sin(x) и y2=sin |x| Рис. 7 см. расчет данных в приложении 1.
|
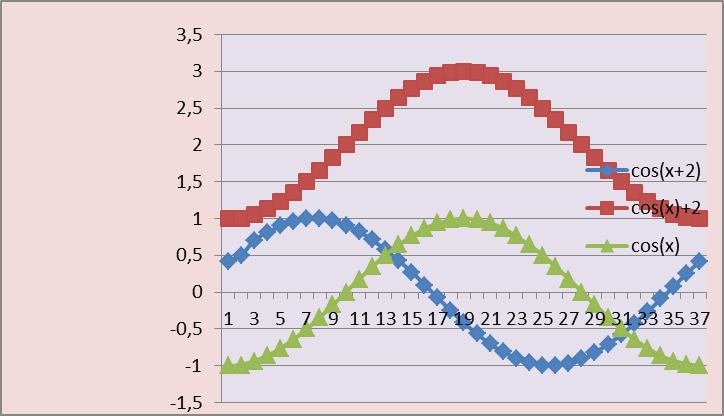
Работают самостоятельно в группах. Отчет группы №1 по Рис.5 cos(x+2): сдвинута вдоль оси X вправо на 2, период 2π, ОДЗ: -1≤Y≤+1, расчет данных для построения графика см. приложение 1. cos(x)+2: сдвигается на 2 вдоль оси Y вверх, период 2π, четная, ОДЗ: 1≤Y≤3, расчет данных для построения графика см. приложение 1. Отчет группы №2 по Рис.6 sin(x-1): сдвинута вдоль оси X влево на 1, период 2π, ОДЗ: -1≤Y≤+1, расчет данных для построения графика см. приложение 1. sin(x)+3: сдвигается на 3 вдоль оси Y вверх, период 2π, нечетная, ОДЗ: 2≤Y≤4, расчет данных для построения графика см. приложение 1. |
|
Этап урока |
Деятельность учителя |
Деятельность учащихся |
|
5.Подведение итогов (3 мин.) |
Вы смогли самостоятельно выполнить задания? Построенные графики тригонометрических функций с помощью электронных таблиц помогли вам осознать свойства данных функций? Просит детей еще раз сформулировать цели, поставленные в начале урока и определить, достигнуты ли они. Оценивает работу групп и работу самых активных учащихся. При выставлении оценки учитывается проведенный анализ функций, объем выполненной работы, самостоятельность выполнения задания, правильность подготовки таблиц и оформления диаграмм. |
Самостоятельно определяют насколько сумели достигнуть поставленных на уроке целей. Мы вспомнили, как из графика функции вида y=F(x) получается график функции y=kF(ax+b)+d, повторили свойства тригонометрических функций (четность, нечетность, периодичность), использовали электронные таблицы для построения графиков функций, убедились в эффективности использования табличного процессора для решения прикладных задач (просто, быстро, удобно!), провели сравнительный анализ построенных графиков функций и определили их свойства.
Слушают замечания и свои оценки. |
|
Домашнее задание (применение нового знания) (2 мин.) |
Задания приготовлены на карточках (приложение 2). В случае необходимости, разъясняет задания. |
Получают домашнее задание. Выходят из кабинета. |
Приложение 1
|
sin(x/3) |
cos(x+2) |
cos(x)+2 |
cos(x) |
sin(x) |
sin(x)+3 |
sin(x-1) |
|x| |
sin|x| |
sin (X) |
|
-0,866025404 |
0,416147 |
1 |
-1 |
-1,22515E-16 |
3 |
0,841471 |
3,141592654 |
1,22515E-16 |
-1,22515E-16 |
|
-0,851116672 |
0,493814 |
1,003805 |
-0,99619 |
-0,087155743 |
2,912844257 |
0,791178 |
3,054326191 |
0,087155743 |
-0,087155743 |
|
-0,802123193 |
0,702048 |
1,060307 |
-0,93969 |
-0,342020143 |
2,657979857 |
0,60593 |
2,792526803 |
0,342020143 |
-0,342020143 |
|
-0,766044443 |
0,815042 |
1,133975 |
-0,86603 |
-0,5 |
2,5 |
0,458584 |
2,617993878 |
0,5 |
-0,5 |
|
-0,727373642 |
0,903272 |
1,233956 |
-0,76604 |
-0,64278761 |
2,35721239 |
0,297305 |
2,443460953 |
0,64278761 |
-0,64278761 |
|
-0,686241638 |
0,964056 |
1,357212 |
-0,64279 |
-0,766044443 |
2,233955557 |
0,126992 |
2,268928028 |
0,766044443 |
-0,766044443 |
|
-0,64278761 |
0,995548 |
1,5 |
-0,5 |
-0,866025404 |
2,133974596 |
-0,04718 |
2,094395102 |
0,866025404 |
-0,866025404 |
|
-0,597158592 |
0,996791 |
1,65798 |
-0,34202 |
-0,939692621 |
2,060307379 |
-0,21992 |
1,919862177 |
0,939692621 |
-0,939692621 |
|
-0,549508978 |
0,967746 |
1,826352 |
-0,17365 |
-0,984807753 |
2,015192247 |
-0,38597 |
1,745329252 |
0,984807753 |
-0,984807753 |
|
-0,5 |
0,909297 |
2 |
6,13E-17 |
-1 |
2 |
-0,5403 |
1,570796327 |
1 |
-1 |
|
-0,44879918 |
0,82322 |
2,173648 |
0,173648 |
-0,984807753 |
2,015192247 |
-0,67821 |
1,396263402 |
0,984807753 |
-0,984807753 |
|
-0,396079766 |
0,712129 |
2,34202 |
0,34202 |
-0,939692621 |
2,060307379 |
-0,79552 |
1,221730476 |
0,939692621 |
-0,939692621 |
|
-0,342020143 |
0,579401 |
2,5 |
0,5 |
-0,866025404 |
2,133974596 |
-0,88865 |
1,047197551 |
0,866025404 |
-0,866025404 |
|
-0,286803233 |
0,429068 |
2,642788 |
0,642788 |
-0,766044443 |
2,233955557 |
-0,95478 |
0,872664626 |
0,766044443 |
-0,766044443 |
|
-0,230615871 |
0,265698 |
2,766044 |
0,766044 |
-0,64278761 |
2,35721239 |
-0,9919 |
0,698131701 |
0,64278761 |
-0,64278761 |
|
-0,173648178 |
0,094255 |
2,866025 |
0,866025 |
-0,5 |
2,5 |
-0,99889 |
0,523598776 |
0,5 |
-0,5 |
|
-0,116092914 |
-0,08005 |
2,939693 |
0,939693 |
-0,342020143 |
2,657979857 |
-0,97552 |
0,34906585 |
0,342020143 |
-0,342020143 |
|
-0,058144829 |
-0,25193 |
2,984808 |
0,984808 |
-0,173648178 |
2,826351822 |
-0,92251 |
0,174532925 |
0,173648178 |
-0,173648178 |
|
0 |
-0,41615 |
3 |
1 |
0 |
3 |
-0,84147 |
0 |
0 |
0 |
|
0,058144829 |
-0,56772 |
2,984808 |
0,984808 |
0,173648178 |
3,173648178 |
-0,73486 |
0,174532925 |
0,173648178 |
0,173648178 |
|
0,116092914 |
-0,70205 |
2,939693 |
0,939693 |
0,342020143 |
3,342020143 |
-0,60593 |
0,34906585 |
0,342020143 |
0,342020143 |
|
0,173648178 |
-0,81504 |
2,866025 |
0,866025 |
0,5 |
3,5 |
-0,45858 |
0,523598776 |
0,5 |
0,5 |
|
0,230615871 |
-0,90327 |
2,766044 |
0,766044 |
0,64278761 |
3,64278761 |
-0,2973 |
0,698131701 |
0,64278761 |
0,64278761 |
|
0,286803233 |
-0,96406 |
2,642788 |
0,642788 |
0,766044443 |
3,766044443 |
-0,12699 |
0,872664626 |
0,766044443 |
0,766044443 |
|
0,342020143 |
-0,99555 |
2,5 |
0,5 |
0,866025404 |
3,866025404 |
0,04718 |
1,047197551 |
0,866025404 |
0,866025404 |
|
0,396079766 |
-0,99679 |
2,34202 |
0,34202 |
0,939692621 |
3,939692621 |
0,219918 |
1,221730476 |
0,939692621 |
0,939692621 |
|
0,44879918 |
-0,96775 |
2,173648 |
0,173648 |
0,984807753 |
3,984807753 |
0,385974 |
1,396263402 |
0,984807753 |
0,984807753 |
|
0,5 |
-0,9093 |
2 |
6,13E-17 |
1 |
4 |
0,540302 |
1,570796327 |
1 |
1 |
|
0,549508978 |
-0,82322 |
1,826352 |
-0,17365 |
0,984807753 |
3,984807753 |
0,678214 |
1,745329252 |
0,984807753 |
0,984807753 |
|
0,597158592 |
-0,71213 |
1,65798 |
-0,34202 |
0,939692621 |
3,939692621 |
0,795518 |
1,919862177 |
0,939692621 |
0,939692621 |
|
0,64278761 |
-0,5794 |
1,5 |
-0,5 |
0,866025404 |
3,866025404 |
0,888651 |
2,094395102 |
0,866025404 |
0,866025404 |
|
0,686241638 |
-0,42907 |
1,357212 |
-0,64279 |
0,766044443 |
3,766044443 |
0,954783 |
2,268928028 |
0,766044443 |
0,766044443 |
|
0,727373642 |
-0,2657 |
1,233956 |
-0,76604 |
0,64278761 |
3,64278761 |
0,991904 |
2,443460953 |
0,64278761 |
0,64278761 |
|
0,766044443 |
-0,09425 |
1,133975 |
-0,86603 |
0,5 |
3,5 |
0,998886 |
2,617993878 |
0,5 |
0,5 |
|
0,802123193 |
0,080052 |
1,060307 |
-0,93969 |
0,342020143 |
3,342020143 |
0,975518 |
2,792526803 |
0,342020143 |
0,342020143 |
|
0,835487811 |
0,251927 |
1,015192 |
-0,98481 |
0,173648178 |
3,173648178 |
0,92251 |
2,967059728 |
0,173648178 |
0,173648178 |
|
0,866025404 |
0,416147 |
1 |
-1 |
1,22515E-16 |
3 |
0,841471 |
3,141592654 |
1,22515E-16 |
1,22515E-16 |
- Построить в одной координатной плоскости графики функций:
- Основные свойства, построенных вами тригонометрических функций:
- Область определения
- Область значений
- Периодичность
- Промежутки возрастания и убывания функции
- Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=sin(x).
- Построить в одной координатной плоскости графики функций:
- Основные свойства, построенных вами тригонометрических функций:
- Область определения
- Область значений
- Периодичность
- Промежутки возрастания и убывания функции
- Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=cos(x).
- Построить в одной координатной плоскости графики функций:
- Основные свойства, построенных вами тригонометрических функций:
- Область определения
- Область значений
- Периодичность
- Промежутки возрастания и убывания функции
- Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=sin(x).
- Построить в одной координатной плоскости графики функций:
- Основные свойства, построенных вами тригонометрических функций:
- Область определения
- Область значений
- Периодичность
- Промежутки возрастания и убывания функции
- Сформулируйте, как в зависимости от изменений коэффициентов происходит растяжение или сжатие графика функции y=cos(x).
- Построить в одной координатной плоскости графики функций:
- Основные свойства, построенных вами тригонометрических функций:
- Область определения
- Область значений
- Периодичность
- Промежутки возрастания и убывания функции
- Построить в одной координатной плоскости графики функций:
- Основные свойства, построенных вами тригонометрических функций:
- Область определения
- Область значений
- Периодичность
- Промежутки возрастания и убывания функции.