Цели урока:
Образовательная:
- знакомство с формулой корней квадратного уравнения, дискриминанта и формирование первичных умений применения ее при решении квадратных уравнений;
- определять количество корней квадратного уравнения в зависимости от знака дискриминанта.
Развивающая:
- развитие математической речи, критического и объективного мышления;
Воспитательная:
формирование познавательного интереса, умения планировать свою работу, формирование объективной самооценки и взаимооценки.
Тип урока: урок изучения нового материала.
Вид урока: урок с применением ИКТ.
Оборудование:
- компьютер;
- мультимедийный проектор;
- презентация,
- раздаточный материал
- "Алгоритм решения квадратного уравнения"
Структура урока
- Организационный момент (1мин)
- Проверка домашнего задания (3мин)
- Устная работа (6 мин)
- Изучение нового материала (15мин)
- Первичное закрепление материала (3мин)
- Странички истории (1мин)
- Физкультминутка (1мин)
- Работа по учебнику (7 мин)
- Самостоятельная работа (5мин)
- Итог урока (2мин)
- Домашнее задание (1мин)
Ход урока
1. Организационный момент.
Ребята! Сегодня тема урока: "Формула корней квадратного уравнения". (Записывается тема урока, слайд ) Эпиграфом нашего урока служат слова двух великих математиков:
Эпиграф к уроку:
Уравнения, как растения, могут иметь корни, а могут и не иметь
А для начала проверим домашнее задание
2. Проверка домашнего задания
Работа 1 ученика показывается с помощью документ-камеры, проверяется всем классом. Остальные проверяют свои решения по своим тетрадям, ошибки исправляют.
3. Актуализация
Устный опрос.
Вопрос 1. Какие уравнения называются квадратными?
(Уравнения вида ax²+bx + c = 0 , где a,b, c – некоторые числа называется квадратным.)
Вопрос 2 . Что значит решить уравнение?
(Решить уравнение – это значит найти все его корни или доказать, что их нет.)
Вопрос 3. Какие из них называются полными, а какие неполными квадратными уравнениями?
(Если коэффициенты b, c отличны от нуля, то уравнение называется полным квадратным уравнением. Если хотя бы один из коэффициентов b, c равен нулю, то уравнение называется неполным.)
Вопрос 4. Перечислите виды неполных квадратных уравнений и расскажите о способах их решения и числе возможных корней уравнений.
|
(Виды неполных квадратных уравнений
|
|
ax² = 0
|
ax²+bx = 0
|
ax²+ c = 0
|
|
Способы решения
|
|
Уравнение всегда имеет один корень, х = 0.
|
Уравнение решается разложением на множители, вынесением общего множителя за скобки. Всегда имеет два корня, один из которых равен нулю.
|
Уравнение решается разложением на множители по формуле разность квадратов, если c < 0 и имеет два противоположных корня. Если c > 0, то уравнение не имеет корней.)
|
Вопрос 5. Практический. Установите соответствие между уравнением и ответом, не решая уравнения.
|
Уравнение
|
|
Ответ
|
|
1. х² - 4 = 0
|
|
А. нет корней
|
|
2. х² + 5х = 0
|
|
Б. 0
|
|
3. х² + 25 = 0
|
|
В. ± 2
|
|
4.2х² - 6х = 0
|
|
Г. – 5; 0
|
|
5. 5х² = 0
|
|
Д. ± 3
|
|
6. 9 – х² = 0
|
|
Е. 0; 3
|
Вопрос 6. Сколько корней может иметь квадратное уравнение?
1. Назовите вид данного уравнения.
2. Назовите его коэффициенты. (12, 72, 108)
4. Изучение нового материала
Мы повторили пройденный материал о неполных квадратных уравнениях, перейдем к полным.
Вопрос 7.
Какие способы решения полных квадратных уравнений вы знаете на данный момент? (Графический способ и способ выделения полного квадрата.)
Какие недостатки этих способов были нами отмечены ранее? (Графический способ не всегда дает точный результат, а способ выделения полного квадрата достаточно сложный и трудоемкий)
А теперь скажите, могли ли математики спать спокойно, если бы для таких нужных и важных уравнений не было бы более простого и универсального способа решения?
Таким образом, цель нашего урока???????
(рассмотреть универсальную формулу для решения квадратных уравнений и научиться ее применять)
Итак, приступим.
Квадратное уравнение имеет видax²+bx + c = 0.
Объясняется на примерах.
ПРИМЕРЫ
Решим три уравнения.
Пример 1.
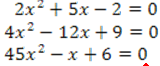
Пример 2.
Пример 3.
Для решения квадратных уравнений используется такое понятие как дискриминант, которое обозначается буквой Д и вычисляется по формуле
D= b2- 4ас
Давайте вычислим для каждого уравнений Д.
Пример 1. Д=49
Пример 2. Д=0
Пример 3. Д<0
ЗНАЧИТ (на доске писать)
Для каждого варианта есть свои формулы для нахождения корня уравнения
|
Д>0
|
Д=0
|
Д<0
|
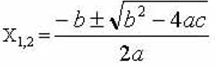 |
Х=
|
Нет решения
|
Давайте найдем для каждого уравнения корни.
Пример 1.
Д=49
Х1=0,5
Х2=-3
Ответ пишем в порядке возрастания. -3; 0,5
Пример 2.
Пример 3.
Пишем в тетрадях (на слайде)
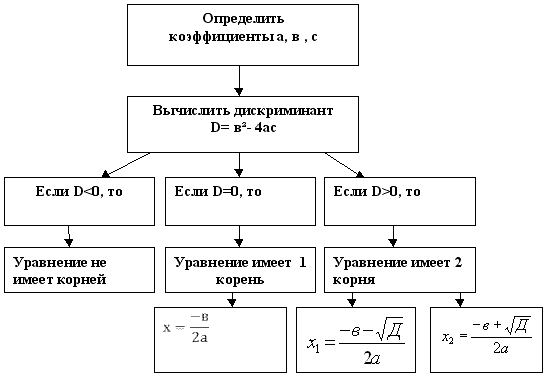
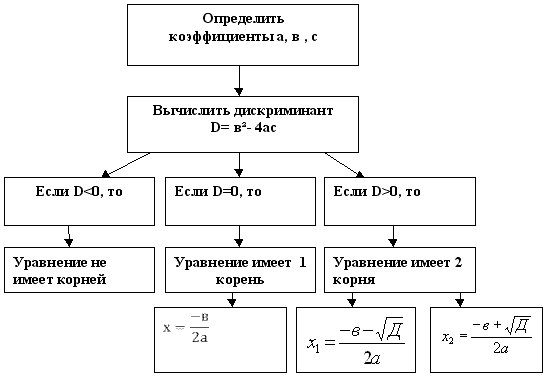
Алгоритм решения квадратных уравнений.
 5. Первичное закрепление материала
5. Первичное закрепление материала 1.Решите уравнения. Задания ОГЭ
Решение у доски (1ученик) --15х+14=0
- 1 вариант 2- 5х +2=0
- 2 вариант -8х - 84=0
Обмениваются тетрадями и взаимопроверка.
6. Странички истории (слайд)
1. Франсуа Виет (1540-1603)
Знаменитый французский ученый. Он впервые установил зависимость между корнями и коэффициентами квадратного уравнения.
3. Кристиан Вольф
Впервые ввёл термин "квадратное уравнение" немецкий философ Кристиан Вольф знаменитый немецкий философ.
4. Сильвестр Джеймс Джозеф английский математик, Сильвестр Джеймс Джозеф, который ввёл термин "дискриминант".
7. Физкультминутка для глаз.
8. Работа по учебнику.
А теперь мы перейдем к работе по учебнику
№25.1 Найти дискриминант квадратного уравнения
№25.3 Определите число корней квадратного уравнения
№25.5 (аб) Решите полное квадратное уравнение
(Учебник Мордкович А.Г.)
9. Самостоятельная работа (на листочках, выполняем с копировкой). Проверяем с помощью Документ-камеры.
Решаем самостоятельно.
|
1 вариант
|
2 вариант
|
|
7-5х-2=0
|
9-12х+4=0
|
Ответы: 1 вариант : -2/7 и 1
2 вариант : 2/3
10. Итоги урока
Давайте подведем итоги нашего урока.
Что же мы сегодня на уроке узнали? (Мы узнали новую формулу для корней квадратного уравнения)
Чему научились? (Мы научились вычислять дискриминант квадратного уравнения и решать его с помощью дискриминанта)
Таким образом, цель нашего урока достигнута. Мы узнали универсальную формулу решения квадратных уравнений, в ее универсальности мы еще не раз убедимся.
Каков алгоритм решения квадратного уравнения?
11.Домашнее задание объясняется.
№ 25.2 Найти дискриминант квадратного уравнения
№ 25.4 Определите число корней квадратного уравнения
№ 25.5(в,г) Решите полное квадратное уравнение
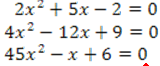
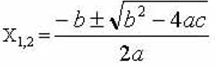
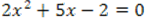
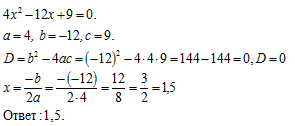
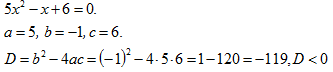
 5. Первичное закрепление материала
5. Первичное закрепление материала