В таких науках как теоретическая информатика и математика в основе умения решать разнообразные задачи лежат ряд базовых алгоритмов, например: умения округлять числа, решать квадратные уравнения, переводить числа из одной системы счисления в другую и т. д. Как правило, для формирования таких базовых умений используются однотипные задачи на прямое применение алгоритма. На традиционном уроке ученикам предлагаются задачи: кто-то решает у доски, остальные в тетради. И не редко у учеников возникает соблазн переписать решение бедумно с доски. Для индивидуализации обучения можно было бы предложить каждому ученику свое собсвенное задание. Но это требует много времени на подбор таких упражнений и на их проверку.
И вот тут на помощь приходит именно однотипность таких заданий. По сути, текст заданий для учеников будет различаться только набором исходных данных. Задачи на прямое применение известного алгоритма как правило формализуемы. А значит, составление задач и проверку можно переложить на компьютер. Конечно, компьютер не заменит учителя полностью. Техника может указать, верен ответ или нет. Но она не сможет объяснить в чем именно ошибся ученик. И все же, использование техники сделает процесс обучения индивидуальным:
- у учеников отличается темп выполнения заданий, то есть учитель может уделять время каждому по мере необходимости;
- ошибки у всех разные, у ученика будет возможность определить, в чем именно для него состоит трудность в усвоении того или иного алгоритма;
- при случайном выборе исходных данных задания не повторяются, а значит нет возможности воспользоваться результатами чужого труда, что позволяет реализовать такие важные дидактические принципы обучения как сознательность и активность;
- одна и та же компьютерная программа может быть использована и в процессе закрепления навыка (учитель помогает ученику, если у него возникают вопросы при выполнении задания) и для проверки полученных знаний (учитель только фиксирует итоговую оценку). Но, подчеркнем, что это возможно только при условии, что задания не повторяются, то есть составляются случайным образом.
Все перечисленные выше идеи были использованы при разработке компьютерной тестовой программы по теме «Системы счисления».
Цель работы – создать программу, которая может генерировать задачи по наперед заданному образцу со случайным набором данных, выбранных из некоторого диапазона, предназначенную для формирования навыка перевода чисел из одной системы счисления в другую.
В данной статье мы рассмотрим только методические аспекты разработки программы, не касаясь технических подробностей.
Задачи, которые должна решать программа:
- выбор типа задач;
- генерациязадач, имеющих единственное решение;
- проверка результатов решения;
- выставление итоговой оценки;
- изменение количества вопросов пользователем в пределах некоторого диапазона;
- невозможность изменения введенного ответа после проверки.
Выбор типа задач. Это, безусловно, основная методическая задача, с которой столкнулся автор в процессе разработки программы. С этой же задачей сталкивается и любой учитель информатики при подготовке к уроку. Обязательными в наборе заданий будут два основных алгоритма: перевод целых чисел из десятичной системы счисления в произвольную и перевод чисел из произвольной системы счисления в десятичную. На более позднем этапе - перевод десятичных дробей. А вот формулировок задач на применение перечисленных выше алгоритмов, также как и задач на понимание сути происходящего, множество. Пока программа предлагает только 5 типов таких заданий, часто встречающихся в различных печатных изданиях. Выбор автора можно назвать субъективным, но программа не претендует на то, чтобы являться единственным средством обучения при прохождении данной темы. Любой учитель может дополнить список задач для решения традиционным способом.
Генерация задач, имеющих единственное решение. Ниже приведены формулировки задач, а также подходы к выбору параметров, а именно: какие параметры задаются случайным образом, а какие параметры расчитываются на их основе; обоснование существования решения полученной задачи и его единственность. При разработке каждого алгоритма учитывались следующие обстоятельства:
- алгоритмы перевода из произвольной системы счисления в десятичную и обратно разработаны и могут быть использованы для написания других алгоритмов;
- целесообразнее случайным образом выбирать десятичное число: для этого предусмотрена стандартная функция, чем реализовывать алгоритм случайного выбора числа в произвольной системе счисления. Чем меньше новых функций, тем меньше вероятность ошибки;
- из тех же самых соображений все арифметические вычисления в рамках программы будем производить в десятичной системе счисления;
- диапазон оснований систем счисления будет задавать пользователь, но программно основание не может быть больше 16.
Вычислить ap +bq. Результат записать в системе счисления с основанием t. В данной задаче 5 независимых друг от друга параметров: a, b, p, q, t. Каждый из них выбираем случайным образом, учитывая, что мы выбираем не сами числа a и b, а их десятичные эквиваленты. Используя эти эквиваленты находим ответ задачи в десятичном виде. Применяя алгоритм перевода чисел из десятичной системы счисления в произвольную, получаем параметры a и b, а также ответ задачи, с которым в последствии программа будет сравнивать ответ, введенный пользователем. Так как каждые действия и фунуции, используемые в рамках данного алгоритма, выполнимы, причем единственным способом, то ответ у сформулированной для конечного пользователя (ученика) задачи существует и он единственный.
В системе счисления с некоторым основанием десятичное число x записывается в виде "abc". Укажите это основание. В данной задаче 2 зависимых друг от друга параметра, поэтому один из них зададим случайным образом, а второй вычислим. Если в качестве случайного выбрать параметр x, то в числе abc может оказаться произвольное количество цифр, что приведет к степенному уравнению, которое решить будет проблематично. В качестве случайного параметра выберем искомое основание системы счисления p. Это же число и будет являться ответом полученой задачи. Зная основание, также случайно выберем три числа: a из диапазона [1; p−1], b, c из диапазона [0; p−1] и переведя число abc в десятичную ситему счисления получим x. Покажем, что p – единственное решение задачи при полученных таким образом abc и x. Действительно, решение задачи сводится к решению уравнения at2 +bt +(c− x)= 0. Это уравнение имеет по крайней мере один корень (по построению задачи). Предположим, что у уравнения имеется еще один корень, отличный от p. Обозначим его p1. Получим:
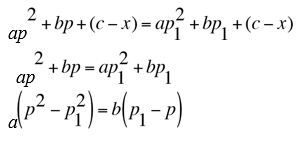
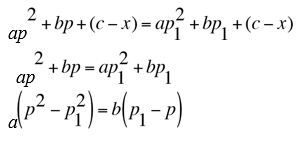
Так как по предположению p≠p1, разделим обе части полученного выражения на p−p1. Получим: a(p+ p1) = −b. Так как b по условию задачи неотрицательно, числа a, p, p1 по условию задачи положительны, то данное равенство возможно только при условии, что p+ p1отрицательно, то есть p1 отрицательно, а значит хотя уравнение и имеет 2 корня, один из них не удовлетворяет условию задачи (основание системы счисления всегда число положительное), то есть задача, которая будет предложена ученику имеет единственное решение.
Запишите числа ap, bq, cf, dt в порядке возрастания (убывания). В ответе укажите числа в десятичной системе счисления. Так же как и в первой рассмотренной задаче, в данном случае мы имеем несколько независимых друг от друга параметров, которые задаем случайным образом в десятичном виде и по необходимости переводим в выбранные системы счисления. Для однозначной трактовки результата дополняем текст задания следуещим требованием: числа в ответе записывать через запятую без пробелов.
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись десятичного числа a оканчивается на b. В данной задаче 2 независимых друг от друга параметра. Наложим на них следующие ограничения: a – некоторое случайное число из диапазона [20;100], b – некоторое случайное число из диапазона [0;15]. Тогда решением будут все делители числа a−b, превосходящие b. Для однозначной трактовки результата дополняем текст задания следуещим требованием: числа в ответе записывать через запятую без пробелов.
Укажите через запятую в порядке возрастания все числа, не превосходящие a, запись которых в p-ичной системе счисления оканчивается на «b». В данной задаче 2 независимых параметра: a и p. Параметр b зависит от p следующим образом: каждая цифра числа b не превышает p−1. Введем следующие ограничения: p задается случайным образом, также случайно выбирается количество цифр f в числе b (от 1 до 4) и само число b; выбираем числоa ∈ [b;b+5⋅ p f ]. Таким образом, в ответе будет не более 6 чисел, каждое из которых находится по формуле: d = b+i⋅ p f , i = 0,5 :d ≤ a. Для однозначной трактовки результата дополняем текст задания следуещим требованием: числа в ответе записывать через запятую без пробелов.
Проверка результатов решения и выставление итоговой оценки. После ввода учеником ответа программа сравнивает его с верным решением и подсчитывает количество верных ответов. Если верно выполнено более 80% заданий ставится оценка «5», от 61% до 80% - оценка «4», от 41% до 60% - оценка «3», в остальных случаях «2». Так как программа вместе с оценкой выводит на экран и количество верных ответов, каждый учитель может назначить свой критерий выставления оценок. Главное, заранее предупредить об этом учеников.
Изменение количества вопросов пользователем в пределах некоторого диапазона. Пользователь может сам задавать количество вопросов, но не более 100.
Невозможность изменения введенного ответа после проверки. Для того чтобы избежать ситуации, при которой ученик после того, как программа выдала правильный ответ на вопрос, изменяет свой вариант ответа и просит защитать решение, ссылаясь на неадекватное поведение программы, проще всего поставить запрет на изменение ответа ученика.
