Демонстрация работы различных сортировок на языке Pascal

Сортировка простыми обменами (сортировка пузырьком).

Сложность алгоритма: O(N²)

Алгоритм состоит из повторяющихся проходов по сортируемому массиву. За каждый проход элементы последовательно сравниваются попарно и, если порядок в паре неверный, выполняется обмен элементов. Проходы по массиву повторяются N-1 раз или до тех пор, пока на очередном проходе не окажется, что обмены больше не нужны, что означает — массив отсортирован. При каждом проходе алгоритма по внутреннему циклу, очередной наибольший элемент массива ставится на своё место в конце массива рядом с предыдущим «наибольшим элементом», а наименьший элемент перемещается на одну позицию к началу массива («всплывает» до нужной позиции как пузырёк в воде, отсюда и название алгоритма).

Сортировка выбором (последовательный поиск минимумов).

Сложность алогоритма: O(N²)

Пусть имеется массив размером N, тогда сортировка выбором сводится к следующему:

1. берем первый элемент последовательности M[i], для первого i равен 1;
2. находим минимальный элемент последовательности и запоминаем его номер;
3. если номер первого элемента и номер найденного элемента не совпадают, тогда два этих элемента обмениваются значениями, иначе никаких манипуляций не происходит;
4. увеличиваем i на 1 и продолжаем сортировку оставшейся части массива, а именно с элемента с номером 2 по N, так как элемент M[1] уже занимает свою позицию;

Сортировка вставками.

Сложность алгоритма: O(N²)

Сначала сортируются два первых элемента массива. Затем алгоритм вставляет третий элемент в соответствующую порядку позицию по отношению к первым двум элементам. После этого он вставляет четвертый элемент в список из трех элементов. Этот процесс повторяется до тех пор, пока не будут вставлены все элементы.

                                                                                                        Сортировка Шелла.
Сложность алгоритма:  O(N²)

Идея метода заключается в сравнение разделенных на группы элементов последовательности, находящихся друг от друга на некотором расстоянии. Изначально это расстояние равно d или N/2, где N — общее число элементов. На первом шаге каждая группа включает в себя два элемента расположенных друг от друга на расстоянии N/2, они сравниваются между собой, и, в случае необходимости, меняются местами. На последующих шагах также происходят проверка и обмен, но расстояние d сокращается на d/2, и количество групп, соответственно, уменьшается. Постепенно расстояние между элементами уменьшается, и на d=1 проход по массиву происходит в последний раз.
Р. Седжвик придумал лучший вариант изменения значений d, которые вычисляются заранее: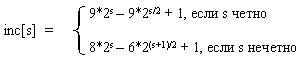

Затем значения d берутся из массива inc с конца.
При использовании таких значений d среднее количество операций:

O(n^7/6), в худшем случае - порядка O(n^4/3).

Сортировка Хоара (быстрая сортировка).
Сложность в среднем случае:  O(NlogN)
Сложность в худшем случае:  O(N²)

Алгоритм:

1. Выбираем в массиве некоторый элемент, который будем называть опорным элементом. С точки зрения корректности алгоритма выбор опорного элемента безразличен.  Известные стратегии: выбирать постоянно один и тот же элемент, например, средний или последний по положению; выбирать элемент со случайно выбранным индексом. 
2. Операция разделения массива: реорганизуем массив таким образом, чтобы все элементы со значением меньшим или равным опорному элементу, оказались слева от него, а все элементы, превышающие по значению опорный — справа от него. 
3. Рекурсивно упорядочиваем подмассивы, лежащие слева и справа от опорного элемента.
4. Базой рекурсии являются наборы, состоящие из одного или двух элементов. Первый возвращается в исходном виде, во втором, при необходимости, сортировка сводится к перестановке двух элементов. Все такие отрезки уже упорядочены в процессе разделения.