Личностные УУД
Задание №1. «Поведение молекул при диффузии».
Цель:раскрыть важнейшее положение молекулярно-кинетической теории: молекулы вещества находятся в непрерывном движении, продолжить работу по формированию умений работать с рисунками и заданиями творческого характера, делать вывод, воспитывать положительное отношение к процессу познания, формирование личностных качеств аккуратность при выполнении работы, бережливость, трудолюбие, логическое мышление.
Возраст: 13–14 лет.
Форма выполнения задания: индивидуальная работа.
Описание задания: задание носит творческий характер. Такая работа развивает у детей логическое мышление, воображение. Формировать такие качества как усидчивость, аккуратность, внимательность.
Материалы: карточка с заданием, карандаши.
Инструкция:
Необходимо нарисовать модели поведения молекул (во времени), объясняющие существование явления диффузии (рис.1) [1].
Критерии оценивания:
- правильность логического мышления;
- аккуратность в выполнение задания.
Задание №2. «Число Пи»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике, формировать положительное отношение к процессу познания, формирование личностных качеств: трудолюбие, логическое мышление, заинтересованность.
Возраст: 11–13 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: задание носит логический характер, даёт возможность для развития творческой деятельности учащихся, в процессе выполнения дети совершенствуют свои знания, вырабатывают умения пользоваться ими, обнаруживают связь математики с жизнью.
Материалы: шаблон круга, нитки, карточка с заданиями.
Инструкция: учащимся предлагается сделать и принести в класс круги различных диаметров. Круг можно сделать из картона и нитки. Ученикам необходимо обвести один из кругов карандашом, затем эту окружность «опоясать» ниткой , а потом распрямить её. Длина нитки будем примерно равна длине данной окружности. Тоже самое проделывают с остальными кругами. Учащиеся сами делают вывод: чем больше диаметр окружности, тем больше её длина. Затем для каждого случая надо найти отношение длины окружности к длине её диаметра. Это отношение одно и то же для всех кругов (вывод делают сами учащиеся). Далее учитель предлагает обозначить это отношение греческой буквой π , длину окружности буквой- С, а диаметр буквой - d. Формулу длины окружности учащиеся формулируют самостоятельно (Рис.2). [2].
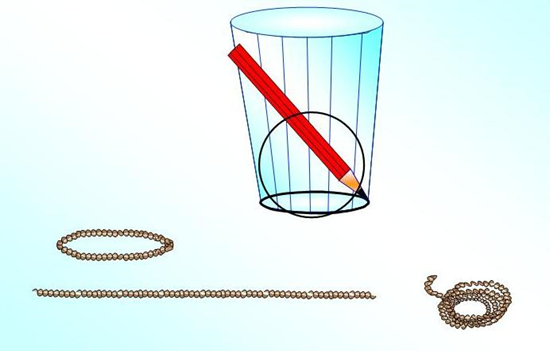
Рис. 2
Критерии оценивания:
Критерии оценивания:
- правильность вычислительных действий;
- способность логического мышления;
- умение прислушиваться к аргументам других участников эксперимента;
- чёткость и содержательность вывода.
Регулятивные УУД
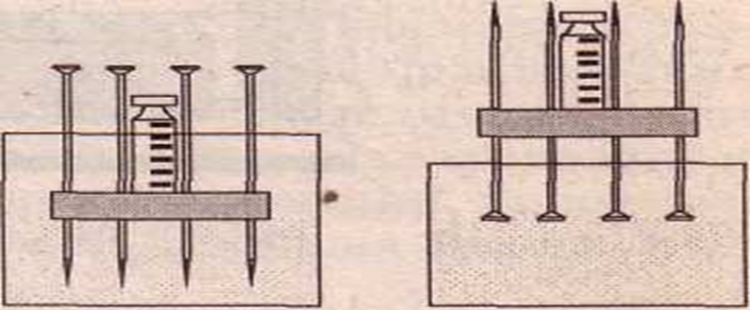
Задание №1 «Давление твёрдых тел»
Цель: Формирование логического мышления, мотивация учения, развитие интереса к физике, расширить естественнонаучную систему взглядов на процессы, происходящие в природе, развитие зрительной памяти, внимания, смысловой памяти, умений анализировать, сравнивать, обобщать.
Возраст: 13–14 лет.
Форма выполнения задания: индивидуальная и групповая работа.
Описание задания: по представленному опыту (Рис.3) учащиеся должны заполнить таблицу, как изменяются величины в каждом из случаев. [1].
Материалы: карточка с заданием.
Инструкция: заполнить таблицу, сделать вывод.
Рис. 3
Рис. 3|
Опыт |
Что увидели |
Сила |
Площадь |
Давление |
|
Дощечка шляпками вниз |
Шляпки гвоздей практически не проваливается |
равная |
большая |
меньшее |
|
Дощечка острием вниз |
Гвозди проваливаются сильнее |
равная |
меньшая |
больше |
|
Дощечка острием вниз и дополнительный груз |
Гвозди проваливаются еще сильнее |
большая |
равная |
ещё больше |
Критерии оценивания:
- анализ движения собственной мысли;
- умение найти и исправить ошибки;
- умение правильно сформулировать вывод;
Задача №2 «Математика в профессии портного»
Цель: обеспечить учащимся возможность управления познавательной и учебной деятельности посредством постановки целей, планирования, контроля, коррекции своих действий и оценки успешности усвоения. Последовательный переход к самоуправлению и саморегуляции в учебной деятельности обеспечивает базу будущего профессионального образования и самосовершенствования.
Возраст:12–13 лет
Форма выполнения задания: групповая работа.
Описание задания: учащимся предлагается решить задачи, используя нестандартные решения.
Материалы: карточки с заданиями.
Инструкция: Жила-была девочка Маша. Она очень любила шить и не очень любила математику.
«А зачем мне математика?» – часто говорила она. «Я уже знаю, кем стану. Я буду портнихой. А портному математика не нужна. Сиди себе и строчи на машинке».
Вот сегодня мы и должны выяснить, нужна ли портному математика.
Задача 1.
Маша имеет кусок ткани длиной в 16 метров, от которого она отрезает ежедневно по 2 метра. По истечении скольких дней она отрежет последний кусок?
Решение. Последний кусок будет отрезан по истечении 7 дней.
Задача 2.
Маша любит шить дома у окна. Это окно квадратное площадью 1 квадратный метр. Но оно пропускает слишком много света. Тогда Маша загородила половину его, но при этом у нее снова осталось квадратное окно в метр шириной и метр высотой. Как это могло получиться?
Решение.
Маша загородила четыре угла, и у нее осталось квадратное окно вдвое меньшей площади, но в метр шириной и метр высотой.
Задача 3.
5 рулонов ткани лежат в корзине. Нужно разделить их между пятью портными так, чтобы каждый получил по рулону, и один рулон остался в корзине.
Решение. Один портной берет рулон вместе с корзиной.
Задача 4.
У Маши дома есть разные отрезы ткани: все, кроме двух, – ситцы; все, кроме двух, – шелка; все, кроме двух, – бязи. Сколько отрезов ткани у Маши?
Решение.
У Маши один отрез ситца, один отрез шелка и один отрез бязи [3].
Критерии оценивания:
- правильность вычисления;
- способность логического мышления;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи.
Коммуникативные УУД
Задание №1 «Геометрический кроссворд»
Цель: включение школьников в эту интеллектуальную игру, позволяет учителю в нетрадиционной форме проверить их знания, прочность и глубину усвоения пройденного, выявить, какие именно вопросы нуждаются в разъяснении и закреплении.
Возраст: 15–17 лет.
Форма выполнения задания: групповая работа.
Описание задания: разделить учеников на 2 команды, задача каждой команды разгадать кроссворд на тему «Любители геометрии» (Рис. 4).
Материалы: лист бумаги.
Инструменты: каждая команда получает лист бумаги, на размышление дается от 20–25 минут. По окончании времени листочки с конструкцией кроссворда и вопросами собираются и передаются команде соперников.
Происходит взаимопроверка результатов.
Рис.4
По горизонтали: 7. Четырёхугольник. 8. Математическое действие. 10. Результат сложения однородных величин. 11. Угол, который больше прямого угла, но меньше развёрнутого. 12. Число, которое иногда получается при делении. 13. Вспомогательная теорема. 15. Одна из основных величин, характеризующих геометрическое тело. 17. Тригонометрическая функция. 19. Расстояние между двумя точками прямой. 20. Число натуральное, или – ему противоположное, или нуль. 24. Отрезок, соединяющий две соседние вершины многоугольника. 25. Единица массы. 26. Точка плоскости, равноудалённая от других точек этой же плоскости. 27. Вывод, который ученик заучивает наизусть. 30. Знак, с помощью которого записывают число. 32. Единица массы драгоценных камней. 33. Площадь квадрата со стороной, равной 1/10 части версты. 34. Многогранник.
По вертикали: 1. Буква греческого алфавита. 2. Прочтите знак I в записи АI ВС. 3. Независимая переменная. 4. Тригонометрическая функция. 5. Расположение отрицательных чисел на координатной прямой от начала координат. 8. Единица длины. 9. Линия на координатной плоскости, Изображающая какую-то зависимость. 14. Число, равное 106. 16. Стороны трапеции. 17. Тело вращения. 18. Поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. 21. Одно из чисел при умножении. 22. Древнейшая русская весовая единица, а в Киевской Руси денежная единица серебра. 23. Правильные треугольные пирамиды. 28. Знак, употребляемый при сравнении величин. 29. Граница, отделяющая на поверхности точки данной фигуры от других точек. 31. Монета достоинством в 3 копейки. 32. Группа цифр в записи числа.
Ответы:
По горизонтали: 7. Трапеция. 8. Сложение. 10. Сумма. 11. Тупой. 12. Остаток. 12. Лемма. 15. Объём. 17. Косинус. 19. Длина. 20. Целое. 24. Сторона. 25. Тонна. 26. Центр. 27. Правило. 30. Цифра. 32. Карат. 33. Десятина. 34. Пирамида.
По вертикали: 1. Омега. 2. Лежит. 3. Аргумент. 4. Синус. 5. Влево. 6. Километр. 9. График. 14. Миллион. 16. Боковые. 17. Конус. 18. Сфера. 21. Множитель. 22. Гривна. 23. Тетраэдры. 28. Равно. 29. Линия. 31. Алтын. 32. Класс. [4].
Критерии оценивания:
- способность логического мышления;
- грамотность написания математических терминов;
Задача №2 «Математик-бизнесмен»
Цель: обеспечить возможности сотрудничества – умение слышать, слушать и понимать партнера, планировать и согласованно выполнять совместную деятельность, распределять роли, взаимно контролировать действия друг друга, уметь договариваться, вести дискуссию, правильно выражать свои мысли в речи, уважать в общении и сотрудничества партнера и самого себя. Умение учиться означает умение эффективно сотрудничать как с учителем, так и со сверстниками, умение и готовность вести диалог, искать решения, оказывать поддержку друг другу.
Формировать последовательный переход к самоуправлению и саморегуляции в учебной деятельности обеспечивает базу будущего профессионального образования и самосовершенствования.
Возраст:16–17 лет
Форма выполнения задания: групповая работа.
Описание задания: Перед началом игры составляются 2–3 команды учащихся.
Вступление: Вы – финансово-кредитивные учреждения, которые осуществляют денежные расчёты и наращивают «капитал». Вы – банки (дайте им название).
Ваша задача: решая экономические вопросы, связанные с деньгами, прибылью, доходами, увеличить свой первоначальный капитал. У вас есть акционеры, которые, отвечая на вопросы, тоже будут приносить вам прибыль.
Материалы: эмблемы банков, картинки с изображением валюты, листы бумаги.
Инструкция: Выбирать управляющих банков, которые имеют право принимать окончательное решение по данному вопросу.
Стартовый капитал каждого банка 100 000 рублей.
Каждому банку предлагается по очереди выбирать себе задание стоимостью от 5 000 до 20 000 рублей.
Время на обдумывание задания предоставляется в зависимости от его сложности.
Каждый акционер может помочь своему банку: за дополнительный правильный ответ капитал банка увеличивается на 5 000 рублей.
Победителем считается тот банк, у которого больше «денег».
Вопросы стоимостью 5 000 рублей:
- Мастерица связала свитер и продала его за 100 рублей. Какую прибыль она получила, если на свитер пошло 3 мотка шерсти по 20 рублей за моток, а на украшение свитера понадобился бисер стоимость 10 рублей. Ответ: 30 рублей.
- Два бизнесмена поспорили: кто получил больше прибыли. Один выручил от продажи своих товаров 5 000 рублей, а его расходы составили 3 000 рублей. Другой бизнесмен наторговал на 1 000 рублей меньше, но и затратил своих денег всего 2 000 рублей. Кто выиграл спор? Ответ: никто.
Вопросы стоимостью 10 000 рублей:
- Коля печет пирожки и продает их на рынке. В 1 день он продал 100 пирожков по цене 10 рублей за один пирог. На следующий день он снизил цену на 10% и продал 110 пирожков. В какой день он заработал больше денег? Ответ: в 1 день.
- Бизнесмен положил в банк 1 000 000 рублей. Через год он забрал из банка 1 500 000 рублей. Какая процентная ставка в этом банке? Ответ: 150%.
Вопросы стоимостью 15 000 рублей:
- Отец обещал сыну за каждую правильно решенную задачу опускать в копилку по 10 рублей, а за каждую неправильно решенную задачу сын должен возвращать отцу по 5 рублей. После того, как было решено 20 задач, у сына в копилке оказалось 80 рублей. Сколько задач сын решил правильно, а сколько неправильно? Ответ: 12 задач решил правильно, а 8 задач – неправильно.
- Вы продаете лимонад. Затраты на производство и реализацию 1 стакана лимонада составляет 30 рублей. По цене 60 рублей можно реализовать 130 стаканов в день, а по цене 50 рублей – 200 стаканов. Какую цену вы должны назначить, если хотите получить больше прибыли? Ответ: 50 рублей за 1 стакан. [4].
Критерии оценивания:
- правильность вычисления;
- способность логического мышления;
- умение выслушать мнение своих товарищей.
Познавательные УУД
Задание №1. «Математика и экология»
Цель: Формирование вычислительных навыков, мотивация учения, развитие интереса к математике, охране окружающей среды. Формировать положительное отношение к процессу познания, формирование личностных качеств: трудолюбие, логическое мышление, заинтересованность. Научить школьников самостоятельному применению знаний в новой ситуации.
Возраст: 11–2лет.
Форма выполнения задания: групповая работа.
Описание задания: Необходимость формирования моделирования как универсального учебного действия. Для математики это действие представляется наиболее важным, так как создаёт важнейший инструментарий для развития у детей познавательных универсальных действий, этому способствует широкое использование продуктивных заданий, требующих целенаправленного использования и, как следствие, развития таких важнейших мыслительных операций, как анализ, синтез, классификация, сравнение, аналогия .
Материалы: карточки с заданием, интернет, энциклопедии по экологии.
Инструкция: Учащиеся делятся на группы, получают карточку с задачей, которую необходимо решить и найти в энциклопедии или интернете дополнительный материал по теме задачи.
Задача №1. По данным ФАО и ЮНЕП, площадь тропических лесов на планете составляет 400 млн.га. Известно, что ежегодно вырубают и сжигают примерно 7 млн.га. Определите, через какое время могут исчезнуть с лица Земли тропические леса, если темп их уничтожения сохранится? (Рис. 5)
Рис.5
Задача №2. Ежегодно весенней порой идёт массовое уничтожение луковичных растений: тюльпанов и первоцветов, которые занесены в Красную книгу. По подсчётам экологов, каждый «цветовод-любитель» срывает более 50 растений. Сколько цветов может сохранить ваш класс, если откажется от этого варварского обычая? (Рис.6)
Рис.6
Задача №3.Из плохо закрытого крана за сутки вытекает до 300 л/ пресной воды [3].
Задача №3.Из плохо закрытого крана за сутки вытекает до 300 л/ пресной воды [3].
Рис.7
Критерии оценивания:
Критерии оценивания:
- способность логического мышления;
- умение прислушиваться к аргументам других участников дискуссии и учитывать их в своей позиции, при решении задачи;
- умение получить и отстоять правильность полученного решения.
Задание №2 «Графики функций – пословицы»
Цель: Формирование познавательных навыков, мотивация учения, развитие интереса к математике. Формировать положительное отношение к процессу познания, формирование личностных качеств: трудолюбие, логическое мышление, заинтересованность. Научить школьников логически мыслить, рассуждать.
Возраст: 16–17 лет.
Форма выполнения задания: индивидуальная, групповая работа.
Описание задания: Занимательные и познавательные задачи с нестандартным решение очень полезны для развития гибкости ума, выработки навыков нешаблонного мышления, повышения интереса к предмету. В таких задачах математики предстаёт перед учащимися новой гранью.
Материалы: карточки с заданиями.
Инструкция: Учащимся предлагаются карточки с графиками функций и пословицы. Необходимо сопоставить график и пословицу и объяснить полученный результат [2].
1. «Повторение-мать учения» (Рис.8).
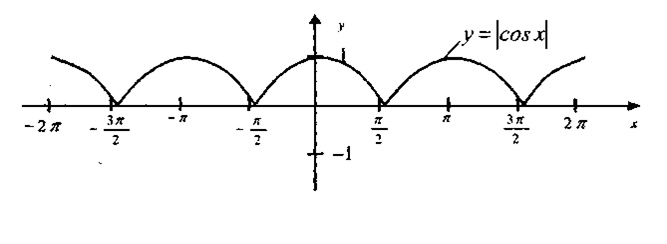Рис. 8
2. «Любишь с горки кататься, люби и саночки возить» (Р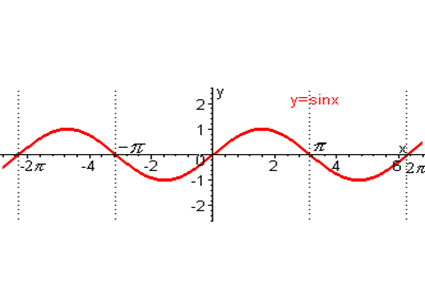ис.9).
Рис.9
3. «Как аукнется , так и откликнется»(Рис.10)
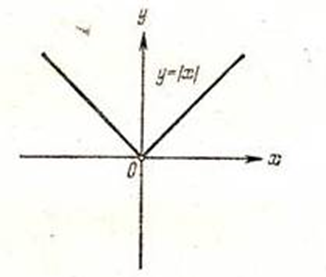
Рис. 82. «Любишь с горки кататься, люби и саночки возить» (Рис.9).
Рис.93. «Как аукнется , так и откликнется»(Рис.10)
Рис.10
Критерии оценивания:
Критерии оценивания:
- способность логического мышления;
- умение прислушиваться к мнениям других участников дискуссии и учитывать их в своей позиции, при решении задачи;
- умение отстоять правильность полученного решения.
Ссылки на источники
- Татьянкин Б.А. Системат индивидуальных заданий по физике для учащихся 7 классов.-Воронеж, 2001 г.
- Барышникова Н.В.Математика 5-11 классы .Игровые технологии на уроках.-Волгоград, издательство «Учитель» ,2007 г.
- Е.А.Ким. Внеклассная работа по математике .-Волгоград, ИТД «Корифей» 2007 г.
- Гончарова Л.В. Предметные недели в школе. Математика. -Волгоград, издательство учитель ,2002 г.
Maslova Irina Viktorovna,
teacher of mathematics and physics, MKO "Nizhnemamonsky school №2", the village Mamon, district Verkhnemamonskiy, the Voronezh region.
teacher of mathematics and physics, MKO "Nizhnemamonsky school №2", the village Mamon, district Verkhnemamonskiy, the Voronezh region.
Irusik96100@yandex.ru
Typical tasks in the formation of universal learning activities in math class
Abstract: The article presents the tasks that contribute to the formation of universal educational activities (personal, educational, regulatory, communication) in mathematics lessons in 5–8 classes by means of different types of problems, examples, games, creative tasks.
Keywords: universal learning activities, learning to learn, assignments, math games, practice skills.