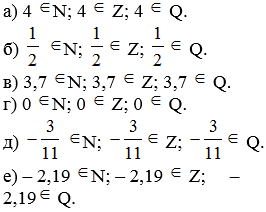- образовательные:
- воспитательные:
- развивающие:
|
Анализ |
Слова учителя |
Слова учеников |
|
I. Организационный момент 1 мин. |
Здравствуйте! Сегодня на уроке математики вас ждет интересная работа по открытию новых знаний. |
|
|
II. Постановка проблемы 6 мин. |
На слайде представлены числа: ; 4; 0,35; 1,23; 1; 0; – 1; ; – 3,18; ; Примечание: ряд чисел взят из учебника № 1178. Внимательно рассмотрите их. Какие числа Вы видите?
Задание. Разбейте данные числа по какому либо признаку на 5 групп, на 4 группы, на 3 группы и на 2 группы. Вы распределяли числа по группам. На что вы обращали внимание? Мы числа разбили на 2, 3, 4 и 5 групп. Ни у кого из вас не возник вопрос? |
Положительные, отрицательные, дроби, натуральные, целые. Учащиеся устно у доски, показывая на числа, делят их на группы.
На запись чисел
Можно ли объединить эти разные по записи числа в одну группу? |
|
III. Поиск решения 7 мин. |
Чтобы числа можно было объединить в одну группу, что для этого нужно? Работа в парах. Задание: примените свои математические знания так, чтобы запись предложенных вам чисел выглядела одинаково. 1 ряд парт: ; 1,23; – 1. 2 ряд парт: 4; ; – 3,18. 3 ряд парт: 0,35; 1; 4 ряд парт: 0; – 3,18; . Выглядят ли записи чисел одинаково? Теперь можно объединить их в одну группу? Как называются числа, записанные таким образом? Какие числа стоят в числителях? Какие числа стоят в знаменателях? Итак, если целое число примем за а и натуральное – за n, то как можно представить запись числа? Слово «дробь» математики могут заменить другим словом. Например, каким? Числа, которые можно записать в данном виде, называются рациональными. Поэтому тема нашего урока …? Какие числа называются рациональными? Сверим ваше определение с определением записанным в учебнике на стр. 202. Термин «рациональное» (число) происходит от латинского слова ratio – «отношение». Целые и дробные числа составляют множество рациональных чисел, которое принято обозначать буквой Q. |
Чтобы запись чисел выглядела одинаково.
Учащиеся выписывают получившиеся результаты на доску.
Да
Да
Обыкновенные дроби
Целые
Натуральные
В виде дроби , где а – целое число, n – натуральное число.
Деление, отношение
Рациональные числа. Учащиеся проговаривают определение. |
|
IV. Практика 10 мин. |
Задание. Верно ли, что …
Задание № 1179. Работаем по рядам. 1 ряд решают примеры под буквой а, 2 ряд – б, 3 ряд – в. Каждый ряд решает по два примера. Сделать вывод: при … рациональных чисел получается число … . Какой общий вывод можно сделать?
Всегда ли частное двух рациональных чисел есть число рациональное? Сверим ваши выводы, с замечаниями записанными в учебнике стр. 202. |
Трое учащихся работают у доски.
Сумма, разность, произведение и частное рациональных чисел тоже число рациональное.
Если делитель отличен от нуля. |
|
V. Физкультминутка 2 мин. |
http://www.youtube.com/watch?v=Cg25Q5qqRUQ
|
|
|
VI. Решение задач 10 мин. |
1) Задание. Выразить обыкновенные дроби в виде десятичных дробей.
2) Запись и чтение периодических дробей стр. 203 о периодических дробях. Как правильно говорить стр. 204.
3) Прочитайте дроби: 0,555; 12,1212; 0,(3); 2,(85); 0,1 (7); 92,56(2)
4) Запишите дроби под диктовку: 0,(5); 0,0(1); 2,(17); 10,(23); 34,3(4).
5) № 1182 (а, б, в) |
Трое учащихся работают у доски.
Двое учащихся работают за доской.
Трое учащихся работают у доски. |
|
VII. Самостоятельная работа с последующей проверкой 5 мин. |
Математический диктант. 1. Покажите, что числа () являются рациональными. 2. Выразите в виде десятичной или периодической дроби числа ().
|
Ученики обмениваются тетрадями с соседом по парте, проверяют решение, выставляют оценку на полях тетради. |
|
IX. Итог урока 2 мин. |
Как формулировалась тема урока? Какие числа называются рациональными? Продолжите фразу: «Я на уроке научился …». |
Рациональные числа |
|
X. Домашнее задание 2 мин. |
П. 37, вопросы, № 1196, 1197, 1200 (а). Творческое задание: составить синквейн «Рациональные числа». |
|