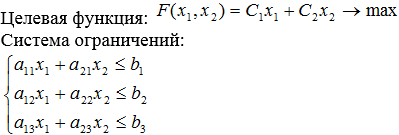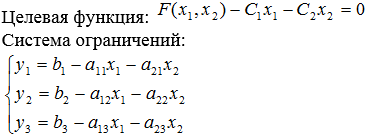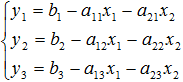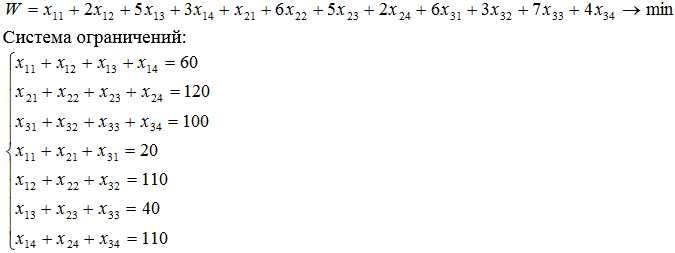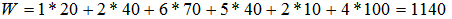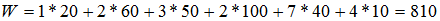ВВЕДЕНИЕ
Методические указания к выполнению курсовой работы по учебной дисциплине «Математические методы» содержат общие требования и рекомендации к курсовой работе для студентов, обучающихся по специальности 09.02.03 «Программирование в компьютерных системах» на очной форме обучения.
Тематика курсовых работ определяется преподавателем дифференцированно, с учетом индивидуальных интересов каждого студента. Выбор учитывает государственный стандарт, направление учебно-методической работы, актуальные направления разработки математического, информационного и программного обеспечения. Студенту предоставляется право выбора одной из тем или предложения своей темы с обоснованием целесообразности ее разработки.
Курсовая работа должна быть подготовлена к защите в срок в соответствии с графиком учебной процесса. К защите курсовой работы предоставляются: курсовая работа, электронная реализация в виде решения задачи оптимизации.
По завершении студентом курсовой работы руководитель проверяет работу, проводится защита курсовой работы с оценкой.
1. ЦЕЛЬ И ЗАДАЧИ КУРСОВОЙ РАБОТЫ
Целью курсовой работы является закрепление и углубление теоретических знаний, изучение математического аппарата и приобретение практических навыков разработки алгоритма и решения задачи оптимизации с помощью выбранного программного средства.
Задачи курсовой работы:
- изучение теоретических основ, определяющих тему курсовой работы;
- анализ возможных подходов и методов решения;
- разработка модели, необходимой для реализации поставленной цели;
- разработка алгоритма решения задачи;
- решение задачи с помощью выбранного программного обеспечения;
- анализ полученных результатов работы.
Методы курсовой работы:
- анализ литературы по теме исследования;
- теоретическое решение проблемы;
- проведение математического моделирования;
- решение задачи с использованием программного обеспечения.
В курсовой работе студент должен показать
знания:
- методов системного анализа описания предметной области;
- математических моделей и методов анализа расчетов, оптимизаций детерминированных и случайных явлений и процессов;
- возможностей программного обеспечения компьютерных систем;
умения:
- выделять существенные моменты задачи;
- разрабатывать математическую модель задачи;
- обосновывать выбор методов решения задачи;
- решать задачу выбранными методами в соответствии с алгоритмами основных методов линейного программирования;
- формулировать выводы по полученным результатам моделирования.
2. ПОСЛЕДОВАТЕЛЬНОСТЬ ВЫПОЛНЕНИЯ РАБОТЫ
Курсовая работа может выполняться с использованием фонда библиотеки, компьютерной техники. Выполнение курсовой работы студента проводится во время практических занятий, предусмотренных учебным планом, и базируется на обобщении ранее выполненных работ.
Руководитель оказывает помощь в выборе темы курсовой работы, разработке плана выполнения работы, проводит регулярные консультации, контролирует ход выполнения работы. Ответственность за выбор того или иного решения, правильность расчетов, оформление работы несет студент. Руководитель предостерегает его от ошибочных решений и характеризует достоинства и недостатки различных вариантов решений, при этом право окончательного выбора предоставляется студенту.
Последовательность выполнения курсовой работы включает следующие этапы:
- уточнение темы;
- утверждение темы предметно-цикловой комиссией дисциплин программного обеспечения;
- анализ теоретических источников;
- выбор методов, моделей, структур и их обоснование;
- определение наборов исходных данных и алгоритмов их обработки;
- решение поставленной задачи на компьютере и получение результатов;
- анализ полученных результатов;
- подготовка к защите курсовой работы;
- защита курсовой работы.
Контроль над работой студента осуществляется руководителем в процессе проведения плановых занятий и консультаций.
4. СОДЕРЖАНИЕ ПРАКТИЧЕСКОЙ ЧАСТИ КУРСОВОЙ РАБОТЫ
В практической части студент должен обосновать выбор метода решения задачи. Практическая часть курсовой работы должна содержать:
- постановку задачи;
- математическую модель задачи;
- решение задачи графическим методом;
- решение задачи симплекс-методом;
- решение транспортной задачи;
- решение задачи с помощью Microsoft Excel;
- решение задачи с помощью пакета MathCad.
В зависимости от вида задачи практическая часть может содержать не все перечисленные ниже компоненты.
После решения задачи различными методами необходимо проанализировать полученные результаты и сделать вывод об эффективности выбранных методов.
4.1 Постановка задачи
Некоторое предприятие, после выполнения основной производственной программы, располагает запасами сэкономленного сырья (трёх видов) S1, S2, S3 соответственно в количествах b1, b2, b3 условных единиц. Из этого сырья может быть изготовлено два вида изделий P1, P2. Известны: Aij – количество единиц Sj – го сырья, идущего на изготовление единицы Рj – го вида изделия.
Таблица 1 - Исходные данные.
|
Вид сырья
|
Запросы сырья
|
Запросы сырья на изделие |
|
|
P1 |
P2 |
||
|
S1 S2 S3 |
b1 b2 b3 |
a11 a12 a13 |
a21 a22 a23 |
|
Доход |
C1 |
C2 |
|
Составить такой план выпуска продукции, при котором доход предприятия от реализации всей продукции будет максимальным.
4.2 Математическая модель
На основе условия задачи составить математическую модель, состоящую из целевой функции и системы ограничений.
Пусть x1 – это количество изделий вида Р1, x2 – количество изделий вида Р2.
Преобразовать математическую модель задачи к стандартному виду: в системе ограничений от неравенств перейти к уравнениям путем введения дополнительных переменных. В результате проведенных преобразований будет получена основная задача линейного программирования.
4.3 Алгоритм решения задачи графическим методом
1) Построить график по системе ограничений.
2) Определить область допустимых решений (ОДР).
3) Построить график целевой функции.
4) Найти оптимальную точку (максимум или минимум): двигать прямую целевой функции параллельно самой себе (вверх или вниз), пока прямая не выйдет за пределы ОДР. Крайняя точка ОДР будет оптимумом.
5) Определить, пересечением каких прямых получена оптимальная точка.
6) Решить систему уравнений.
7) Подставить неизвестные в уравнение целевой функции.
8) Сделать вывод о результатах.
9) В случае нескольких подозрительных на оптимум точек, проверить все случаи, и из них выбрать оптимальное решение по результату целевой функции.
4.4 Алгоритм решения задачи симплекс методом
Преобразовать модель к основной задаче линейного программирования. Пусть имеются базисные переменные y1, y2, y3 и свободные x1, x2, тогда систему линейных ограничений всегда можно привести к виду.
Составить симплекс таблицу на основе основной задачи линейного программирования.
Выделить разрешающий столбец xi, разрешающую строку yj, разрешающий элемент aij.
Вычислить величину обратную разрешающему элементу и записать ее в правый нижний угол ячейки.
Остальные элементы разрешающего столбца разделить на разрешающий элемент aij, и результат записать в правый нижний угол.
Остальные элементы разрешающей строки разделить на разрешающий элемент aij, и результат с противоположным знаком записать в правый нижний угол.
В правый нижний угол всех остальных клеток таблицы поместим результат умножения верхнего элемента разделяющей строки, полученного при проведении проекции из рассматриваемой клетки на разделяющую строку, на нижний элемент разрешающего столбца, полученный при проведении проекции из рассматриваемой клетки на разрешающий столбец, т.е. для клетки ysxp имеем - проекция из этой клетки на разрешающую строку ys определяет выделенный элемент разделяющей строки aip и проекция этой клетки на
Сформировать новую таблицу:заменить в её заголовках yi на xj и наоборот;
- в новые строку xj и столбец yi вписать нижние числа из разрешающей строки yi и разрешающего столбца xi исходной таблицы;
- в новые строку xj и столбец yi вписать нижние числа из разрешающей строки yi и разрешающего столбца xi исходной таблицы;
- в остальные клетки таблицы записать разность чисел находящихся в верхней и нижней части в соответствующей клетки исходной таблицы.
Реализация действий 3-7 продолжается до тех пор, пока в строке целевой функции не будут получены положительные коэффициенты при свободных переменных.
4.5 Решение задачи с помощью Microsoft Excel
1. Ввод условий задачи:
1. Ввод условий задачи:
- создание формы для ввода условий задачи;
- ввод исходных данных;
- ввод зависимостей из математической модели;
- назначение целевой функции;
- ввод ограничений и граничных условий.
Таблица 2 – Ввод условий задачи.
|
|
A |
B |
C |
D |
E |
F |
|
1 |
имя |
x1 |
x2 |
ЦФ |
|
|
|
2 |
значение |
|
|
=B2*B5+C2*C5 |
|
|
|
3 |
ниж.гр. |
|
|
|
|
|
|
4 |
верх.гр. |
|
|
|
|
|
|
5 |
коэф.цф |
С1 |
С2 |
|
|
|
|
6 |
|
ограничения |
лев.часть |
знак |
пр.часть |
|
|
7 |
S1 |
а11 |
а21 |
=B7*$B$1+C7*$C$1 |
b1 |
|
|
8 |
S2 |
а21 |
а22 |
=B8*$B$1+C8*$C$1 |
b2 |
|
|
9 |
S3 |
а31 |
а32 |
=B9*$B$1+C9*$C$1 |
b3 |
|
2. Решение задачи:
- установить курсор в ячейку значения целевой функции;
- выполнить команду Сервис, Поиск решения;
- заполнить диалоговое окно поиска решения в соответствии с математической моделью задачи;
- на вкладке Параметры определить пункты Неотрицательные значения и Линейная модель;
- нажать кнопку выполнить;
- в окне результаты поиска решения выбрать Сохранить найденное решение.
3. Проанализировать полученные результаты.
3. Проанализировать полученные результаты.
4.6 Решение задачи с помощью пакета MathCad
4.7 Решение транспортной задачи
Имеются три поставщика и четыре потребителя. Мощность поставщиков и спросы потребителей, а также затраты на перевозку груза для каждой пары «поставщик – потребитель» сведены в таблицу поставок.
Необходимо определить оптимальный план перевозок, чтобы затраты были минимальными.
Таблица 3- Исходные данные транспортной задачи.
|
Поставщик |
Мощность поставщика |
Потребители и их спрос |
|||
|
В1 |
В2 |
В3 |
В4 |
||
|
20 |
110 |
40 |
110 |
||
|
А1 |
60 |
1 |
2 |
5 |
3 |
|
А2 |
120 |
1 |
6 |
5 |
2 |
|
А3 |
100 |
6 |
3 |
7 |
4 |
Математическая модель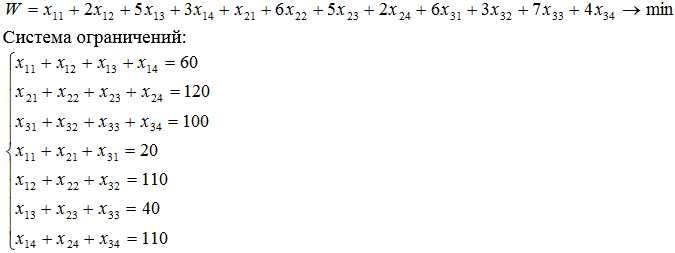
Транспортная задача является сбалансированной, так как 60+120+100=20+110+40+110, 280=280.
Метод северо-западного угла
Для решения задачи заполняется таблица по следующему алгоритму: вывозится груз из пункта А1 в пункт В1 – этой перевозке х11 присваивается максимально возможное значение; если заявка пункта В1 выполнена, а пункте А1 остается груз, то он вывозится в пункт В2; если в пункте А1 не достаточно груза для В1, то недостающий груз берется из А2; после того как спрос потребителя удовлетворен, пункт выпадает из рассмотрения. Процесс заполнения клеток таблицы продолжается до тех пор, пока последняя клетка не будет заполнена, а все спросы не будут удовлетворены, запасы вывезены.
Таблица 4 - Решение транспортной задачи методом северо-западного угла.
|
Мощность поставщика |
Потребители и их спрос |
|||||||
|
1 |
2 |
3 |
4 |
|||||
|
20 |
110 |
40 |
110 |
|||||
|
60 |
1 |
20 |
2 |
40 |
5 |
|
3 |
|
|
120 |
1 |
|
6 |
70 |
5 |
40 |
2 |
10 |
|
100 |
6 |
|
3 |
|
7 |
|
4 |
100 |
Значение целевой функции:
Метод минимального элемента
Заполнение клеток транспортной таблицы начинается с той клетки, в которой значение минимально. В нее записывается максимально возможное значение перевозки хij, которое может быть равно либо запасу Аi, либо заявке Вj. Если заявка Вj выполнена полностью, то j-й столбец больше не рассматривается. Если не вывезенный груз еще остался, то он вывозится в пункт с наименьшим тарифом.
Таблица 5 - Решение транспортной задачи методом минимального элемента.
|
Мощность поставщика |
Потребители и их спрос |
|||||||
|
1 |
2 |
3 |
4 |
|||||
|
20 |
110 |
40 |
110 |
|||||
|
60 |
1 |
|
2 |
60 |
5 |
|
3 |
|
|
120 |
1 |
20 |
6 |
|
5 |
|
2 |
100 |
|
100 |
6 |
|
3 |
50 |
7 |
40 |
4 |
10 |
Значение целевой функции:
Распределительный метод (метод потенциалов)
Подход к решению вопроса оптимальности базисного решения (методов северо-западного угла и минимального элемента) может быть выражен в критерии оптимальности, сформулированном на основе того, что коэффициенты целевой функции должны быть неотрицательными.
Критерий оптимальности: базисное распределение поставок оптимально тогда и только тогда, когда оценки всех свободных клеток неотрицательны.
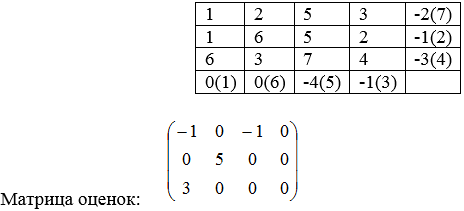
Решение транспортной задачи распределительным методом реализуется по следующему алгоритму: выбирается базисное решение (решение методом минимального элемента); составляется матрица оценок; составляется цикл перерасчета – переменную, при которой коэффициент отрицательный, переводят в базисную. Процесс реализации алгоритма продолжается до тех пор, пока матрица оценок не будет иметь отрицательные оценки.
Найдем оценки свободных клеток по выше приведенному примеру.
Начнем с первого столбца. Пусть потенциал этого столбца равен нулю. Рядом с потенциалом в скобках записываем номер шага (поставки опускаем).
После прибавления этого потенциала к коэффициентам затрат первого столбца коэффициент затрат заполненной клетки (2,1) не измениться; чтобы полученный после сложения коэффициент стал равен нулю, потенциал второй строки должен быть равен -1; для обнуления клетки (2,4) потенциал четвертого столбца должен быть равен -1 и т.д. Измененные коэффициенты затрат удобно записать в виде матрицы оценок. Элементы матрицы оценок, соответствующие свободным клеткам таблицы поставок, равны оценкам этих свободных клеток.
Оценки составляются следующим образом (на примере первой строки матрицы): 0-2+1=-1, 0-2+2=0, -4-2+5=-1, -1-2+3=0.
Для фиксированного базисного решения можно подобрать различные наборы потенциалов, удовлетворяющие правилу 2, однако во всех случаях матрица оценок будет одинаковой.
На основе матрицы оценок, можно сделать вывод, что найденное решение не оптимально. Далее поступаем так, как если бы решали задачу симплекс методом. Переменную х13, коэффициент при которой отрицательный будем переводить в базисную. Перевод поставки в свободную клетку вызывает перераспределение поставок (передвижение поставки по циклу). Получается означенный цикл перерасчета: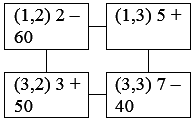
Увеличиваем поставку в клетке (1,3) до тех пор, пока поставка в одной из заполненных клеток не станет равной нулю. Если в клетку (1,3) передать поставку z, то поставка в клетках цикла со знаком + увеличиться на z, а в клетках со знаком – уменьшиться на z. Поэтому искомая клетка находится среди клеток цикла, имеющих знак «-». Более того, она имеет минимальную поставку среди таких клеток. Так как Min{60,40}=40, то клетка (3,3) является искомой. Для обнуления поставки в этой клетке по циклу следует передать 40 единиц груза. После этого клетка (1,3) считается заполненной, а (3,3) - свободной.
Поставка, передаваемая по циклу, определяется как минимум среди поставок в клетках цикла со знаком «-».
В клетках со знаком + цикла поставка увеличивается на передаваемую поставку: поставка клетки (3,2) станет равной 90, поставка клетки (1,3) – 40. Аналогично, в клетках со знаком «-», поставка уменьшиться на передаваемую поставку: поставка клетки (1,2) станет равной 20.
Далее составляется новая таблица распределения поставок и вновь возникает вопрос об оптимальности распределения поставок. Найдем оценки свободных клеток распределения поставок.
Так среди свободных клеток есть клетка (1,1) с отрицательной оценкой, то найденное распределение не оптимально и передача поставки в клетку (1,1) ведет к уменьшению суммарных затрат на перевозку. Означенный цикл пересчета для клетки (1,1) приведен слева. Поставка, передаваемая по циклу равна min{20,20,10}=10. Передвигая поставку по циклу, получаем новое решение. Найдя матрицу оценок, заключаем, что оно оптимально, так как среди свободных клеток нет отрицательных.
Суммарные затраты распределения равны:
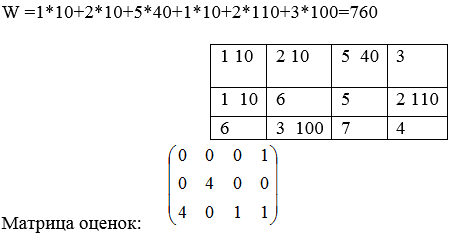Решение транспортной задачи с помощью Microsoft Excel
1) Ввод условий транспортной задачи:
|
|
A |
B |
C |
D |
E |
|
1 |
1 |
2 |
5 |
3 |
60 |
|
2 |
1 |
6 |
5 |
2 |
120 |
|
3 |
6 |
3 |
7 |
4 |
100 |
|
4 |
20 |
110 |
40 |
110 |
|
2) Ввод формул для транспортной задачи:
|
|
A |
B |
C |
D |
E |
F |
G |
|
7 |
|
|
|
|
=СУММ(A7:D7) |
|
Целевая функция |
|
8 |
|
|
|
|
=СУММ(A8:D8) |
|
=СУММПРОИЗВ(A1:D3;A7:D9) |
|
9 |
|
|
|
|
=СУММ(A9:D9) |
|
|
|
10 |
= СУММ (A7:A9) |
= СУММ (B7:B9) |
= СУММ (C7:C9) |
= СУММ (D7:D9) |
|
|
|
3) Решение транспортной задачи:
- установить курсор в ячейку значения целевой функции;
- выполнить команду Сервис, Поиск решения;
- заполнить диалоговое окно поиска решения в соответствии с математической моделью задачи;
- на вкладке Параметры определить пункты Неотрицательные значения и Линейная модель;
- нажать кнопку выполнить;
- в окне результаты поиска решения выбрать Сохранить найденное решение.
4) Вывод решения транспортной задачи:
|
|
A |
B |
C |
D |
E |
F |
G |
|
7 |
10 |
10 |
40 |
0 |
60 |
|
Целевая функция |
|
8 |
10 |
0 |
0 |
110 |
120 |
|
760 |
|
9 |
0 |
100 |
0 |
0 |
100 |
|
|
|
10 |
20 |
110 |
40 |
110 |
|
|
|
5. ПОДГОТОВКА КУРСОВОЙ РАБОТЫ К ЗАЩИТЕ И ПОРЯДОК ЗАЩИТЫ
Оформленная курсовая работа представляется студентом преподавателю для просмотра в соответствии с графиком учебной работы до защиты.
График защиты курсовых работ составляется преподавателем и доводится до сведения студентов. Защита назначается в компьютерных классах, где есть необходимое техническое (персональный компьютер, мультипроектор) и программное обеспечение (Microsoft Office, MathCAD) для демонстрации результатов работы.
Во время защиты курсовой работы студент должен кратко сформулировать цель работы, изложить содержание, акцентируя внимание на наиболее важных и интересных с его точки зрения решениях, в первую очередь, принятых студентом самостоятельно. При выступлении может быть использована демонстрация решения с помощью выбранного программного обеспечения. Защита курсовой работы может быть представлена в виде презентации, где рассмотрены основные методы решения задачи.
Оценка знаний предполагает дифференцированный подход к студенту, учет его индивидуальных способностей, степень усвоения и систематизации основного понятийного аппарата, знаний курса и диагностических навыков, умения делать доказательные выводы и обобщения. Оцениваются не только глубина знаний основных проблем, но и умение использовать в ответе теоретический и практический материал из курсовой работы, активное участие в беседе.
Результаты работы оцениваются с учетом качества ее выполнения и ответов на вопросы по четырехбалльной системе (отлично, хорошо, удовлетворительно, неудовлетворительно).
Таблица 6 - Календарный график выполнения курсовой работы.
|
№ недели |
Вид работы и ее содержание |
Кто осуществляет контроль |
|
1 |
Ознакомление с тематикой курсовых работ |
Руководитель курсовой работы |
|
2 |
Выбор и утверждение темы курсовой работы |
Председатель ПЦК дисциплин программного обеспечения |
|
3-5 |
Работа над теоретической частью курсовой работы |
Руководитель курсовой работы |
|
6-7 |
Практическая часть: постановка задачи и составление математической модели задачи, приведение задачи к каноническому виду |
Руководитель курсовой работы |
|
8 |
Практическая часть: решение задачи графическим методом. |
Руководитель курсовой работы |
|
9 |
Практическая часть: решение задачи симплекс методом. |
Руководитель курсовой работы |
|
10-11 |
Практическая часть: решение задачи с помощью Microsoft Excel. |
Руководитель курсовой работы |
|
12 |
Практическая часть: решение задачи с помощью пакета MathCAD. |
Руководитель курсовой работы |
|
13 |
Анализ результатов решения задачи. |
Руководитель курсовой работы |
|
14-15 |
Оформление курсовой работы. |
Руководитель курсовой работы |
|
16 |
Подготовка к защите курсовой работы. |
Председатель ПЦК дисциплин программного обеспечения |
|
17 |
Защита курсовой работы. |
Председатель ПЦК дисциплин программного обеспечения, руководитель курсовой работы |
Ссылки на источники
- Абуталипов Р.Н. Excel от X до L. — М.: ГроссМедиа, 2017. — 392 c.
- Исследование операций: задачи, принципы, методология: учебное пособие / Е.С.Вентцель. — Москва: ЮСТИЦИЯ, 2018. — 192 с.
- Исследование операций в экономике: учебник для академического бакалавриата / под ред. Н. Ш. Кремера. — М.: Издательство Юрайт, 2018. — 438 с.
- Половко А. Mathcad для студента. — М.: БХВ-Петербург, 2016. — 336 c.